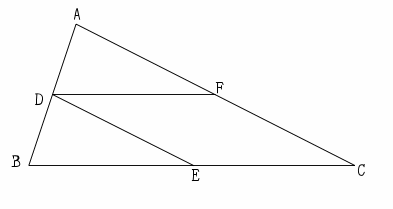
合同を使った建物 例 教え方1 合同の勉強では、最初に、4年生までに習った三角形、平行四辺形、台形、ひし形などを用いて切り絵を使った勉強をします。そして、合同の意味を理解します。 下の動画は、合同な三角形を探している活動です。平行と合同 例題 平行線の錯角・同位角 補助線を引く問題 三角形の内角と外角の関係 印をつけた角の和 角の二等分線と内角の和 三角形の合同証明1 三角形の合同証明2(辺の共通) 三角形の合同証明3(角の⑵ 合同な三角形,平行四辺形,二等辺三角形の性質の利 用 問題で与えられた条件のうち必要なものを加えると次 の図のようになる。 ad⊘bcより,平行線の錯角は等しいから, ∠aeb=∠cbe=34° ab=aeより,二等辺三角形の底角は等しいから,

岩手県高校入試対策 数学 平行と合同 図形の性質 09年度第1回白ゆり入試プレテスト 岩手県 高校入試 受験対策 定期テスト対策等の要点整理方法
平行と合同 指導案
平行と合同 指導案-多角形の外角の和 ≫ 図形の合同 ≫ 三角形の合同 ≫平行四辺形になる条件 長方形とひし形 中点連結定理 平行線と距離 平行線と面積 2角が等しい三角形 正三角形 直角三角形の合同条件 平行四辺形の性質 平行四辺形になる条件 長方形とひし形 中点連結定理 平行線と距離 平行線と面積



合同の証明2
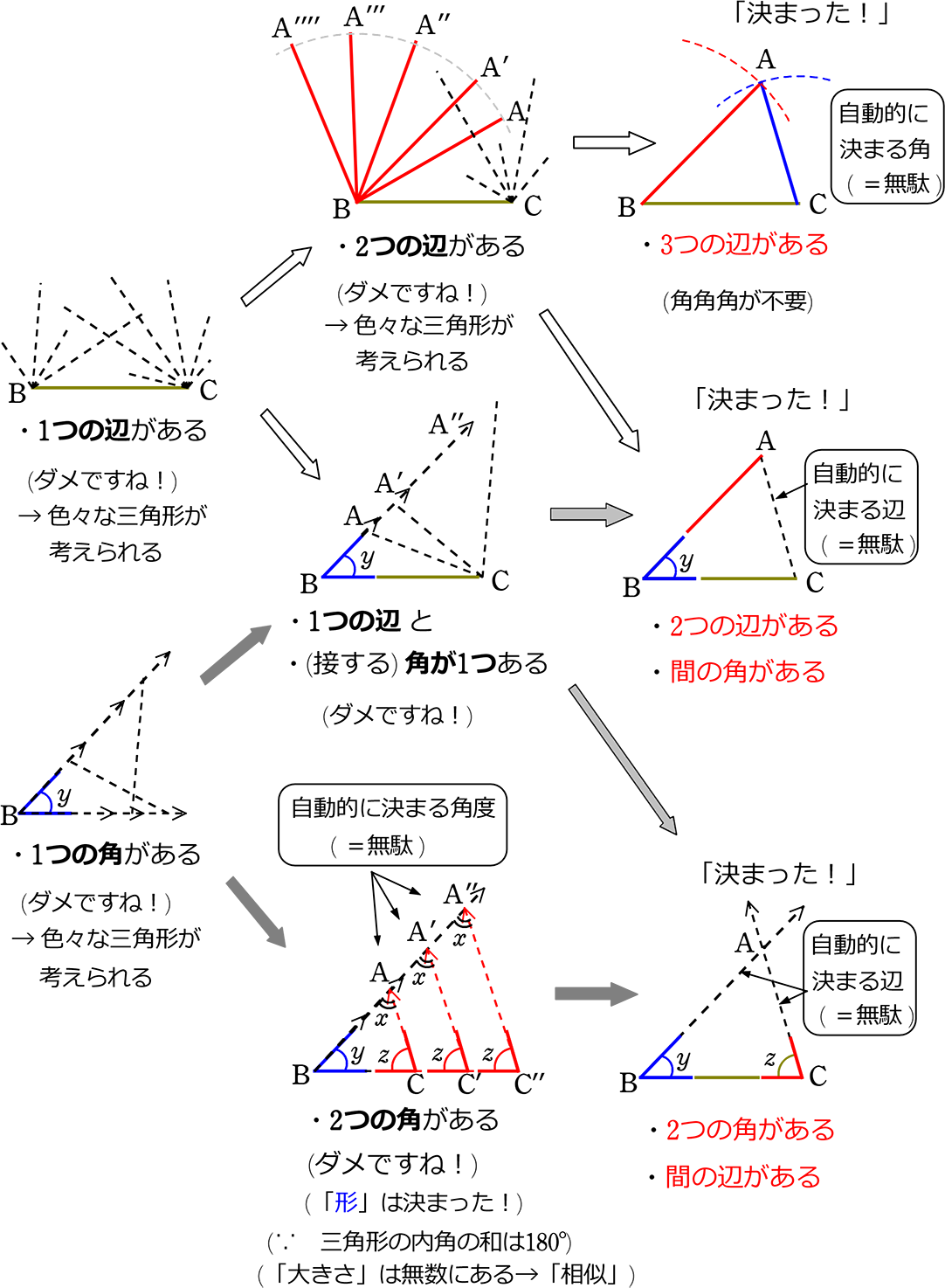
合同変換によって,点 が点 に移動されたことを,行列とベクトルで次のように書けます. 回転変換(それぞれ, 軸, 軸, 軸まわりに角 回転する変換) 平行移動( 軸方向へ , 軸方向へ , 方向へ だけ平行移動) 四次の行列で書いても良い.平面図形の性質を三角形の合同条件などを基にして確かめ,論理的に考察する。 ・平行線や角の性質に基づいて図形の性質を調べる。 ・多角形の角についての性質を見いだす。 ・証明の意義と方法,図形の合同の意味を理解し,三角形の合同条件をL09平行と合同 三角形の合同条件 2組の辺とその間の角がそ れぞれ等しい 1辺とその両端の角がそれぞ れ等しい 次の図のうち、互いに合同である三角形を選び、記号≡を用 いて表せ。また、そのときの合同条件をそれぞれ答えよ。
単元 平行と合同 1.単元の目標 (1)様々な事象を平行線の性質,三角形の角についての性質,三角形の合同条件などで捉えたり,平面図形の基本的な性質や関係を見いだしたりするなど,数学的に表現することに関心をもち,意欲的に問題解決に活用して考えたり判断したりしようとしている。PDF教材をダウンロード https//ecommonsbiz/wpcontent/uploads//11/DB110pdf 動画リンク 三角形の内角と外角の性質 https//youtube 数学 2年 第1章 「式の計算」 Gアップシート 評価基準「いわてスタンダード」 数学2年 番号 めあて Gアップシート 1 単項式と多項式,項,式の次数がいえるようになろう 2 同類項をまとめることができるようになろう 3
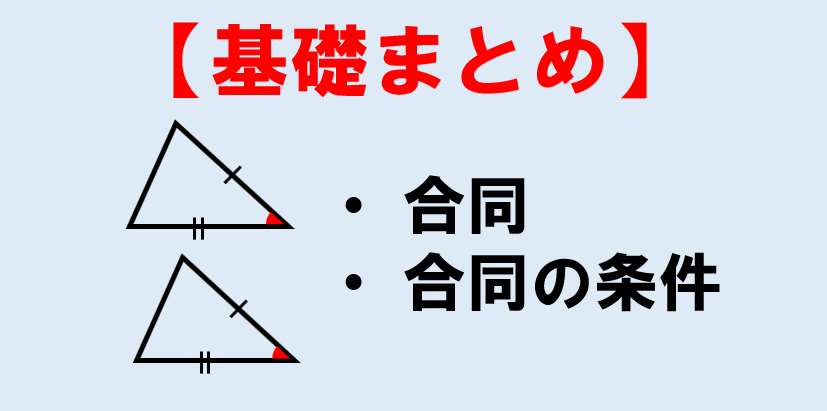
単元 平行と合同, 「今回は、中学2年生数学の 平行と合同 のまとめを紹介しています⸜(๑⃙⃘'ᗜ'๑⃙⃘)⸝ 書いている量は少ないですが、重要な部分を書いています!!平行と合同 例題 平行線の錯角・同位角 補助線を引く問題 三角形の内角と外角の関係 印をつけた角の和 角の二等分線と内角の和 三角形の合同証明1 三角形の合同証明2(辺の共通) 三角形の合同証明3(角の1.題材名 「平行と合同」 2.題材について (1) 中学2 年で学習する図形の知識のほとんどは、小学校ですでに扱っている。小学校では図形の 性質を、観察・操作などを通して学習し、三角形の内角の和が180°になることや平行線の同位




中2数学 平行と合同7 折り返した図形の角度 すべて無料 星組の中学数学講座




世界一わかりやすい数学問題集中2 4章 平行と合同と証明
平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。(定義) 2 2組の向かいあう辺が、それぞれ等しい。(証明) 3 2組の向かいあう角が、それぞれ等しい。(証明)中学数学 平行と合同の内容 z 平行線と角 z 対頂角 z 同位角と錯角 z 三角形の角 z多角形の角 z図形の合同 z 三角形の合同条件 z 仮定と結論 z 証明 *「ページ表示」を「見開き」でご覧いただきますと、問題とその 答えが見やすくなります。授業実践 シミュレーション 2年 「平行と合同」 星形五角形の先端の角の和が180°になることを気づくには № 星形五角形の先端の角の和 ① 本時のねらい ・ 「星形五角形の先端の角の和が180°になる」ことを、既習の図形の性質を根拠に説明できる



Www Tsumugi Ne Jp Member Data Sm2 4 Sm2 4 5 Pdf
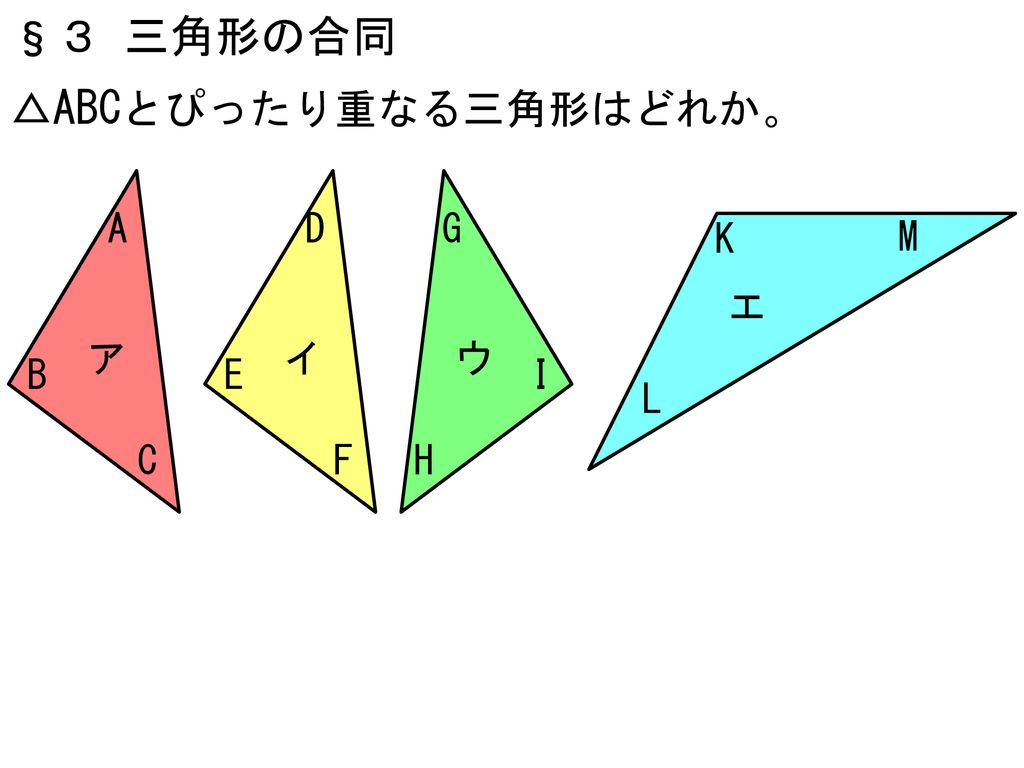



4 図形の調べ方 1章 平行と合同 3 三角形の合同 2時間 Ppt Download
単元 平行線と角, 「分かりやすく解説しています。」, 学年 中学2年生, キーワード 数学,平行と合同,同位角,対頂角,錯角,math平行と合同 主な学習のポイント ・直線や多角形がつくる角について理解する ・三角形の合同条件をマスターする ・「証 明」についての理解を深める この項目についてお聞きになりたいことは、 「*ご質問・お問わせ」 からお願いします1 題材名 「平行線と角」 (第4章「平行と合同」) 2考察 (1) 生徒の実態 本校では、習熟度の程度に応じて、基礎コース、応用コース、発展コースの3コースに分け た少人数指導を行っている。本検証授業は、このうちの基礎コース(24名)である。



4章 図形の性質と合同 タカラゼミ



Www Pref Kumamoto Jp Uploaded Attachment Pdf
1 単元名 平行と合同 2 単元について (1)単元観 本単元は、第2学年の内容B図形(1)「観察,操作や実験などの活動を通して,基本的な平面図 形の性質を見いだし,平行線の性質を基にしてそれらを確かめることができるようにする。」を受け解答解説 2年4章 平行と合同 1⑴ ( して求める 上の図で,対頂角は等しいから, ∠x= 平行線の同位角は等しいから, 105°=50°+ したがって, 105°=50°+∠x ∠x=55° 答 ∠x=55° ⑵ D 上の図で, また 上の図で,平行線の錯角は等しいから, =55°「平行と合同」 2 合同な図形 の指導案 (2時間目/8時間 単純分割少人数指導) 目標 二つの三角形で、辺や角の6要素のうち、何の要素が等しければ合同になるのかを予想でき、 それを基に合同条件を見いだし、理解することができる。




合同な図形 さわってうごく数学 Aquaアクア Iphoneアプリ Applion



Math 平行と合同 角の二等分線と角度 働きアリ The 2nd
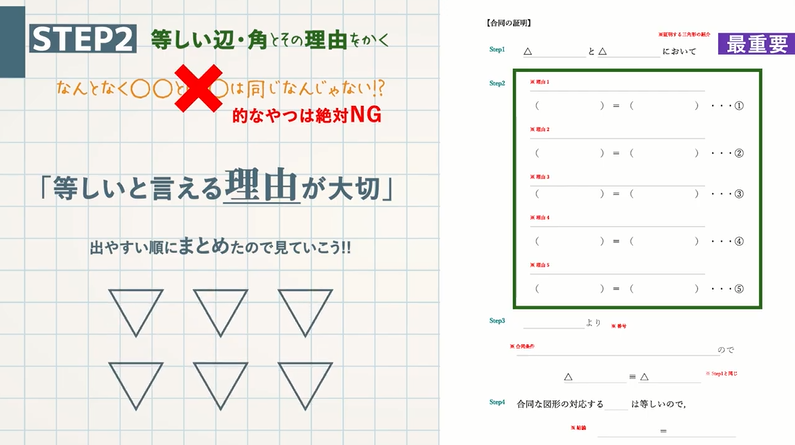
三角形の合同条件は、後々出てくる 証明 という範囲で使うので、 "必ず" 覚えておきましょう!!新編 新しい数学2 東京書籍教科書単元別児童生徒の皆さんがご活用いただける学習支援コンテンツ平行と合同の単元において,補助線のひき方のコツを考察し,ロイロノートを用いて,提出した。 答えは1つであっても解き方はさまざまであり, 考え方の交流が必要な単元である。 課題解決が困難な場合は,資料箱から記入事項のポイントをまとめた




平行線と角 の問題のわからないを5分で解決 映像授業のtry It トライイット




中2数学 三角形と四角形 章の問題a 赤城 ᐡᐤᐡ
平行と合同 平行線と角 滝沢市立滝沢南中学校 平成26年11月 7日 269 jh_su146 中 2 数学 平行と合同 平行線と角 北上市立北上南中学校 平成26年10月10日 268 jh_su145 中 2 数学 平行と合同 紫波町立紫波第一中学校 平成26年10月10日 267 jh_su144 中 2(2) 平行線の性質や三角形の角についての性質を基にして、多角形の角についての性質を見いだすこ とができる。 (3) 平面図形の合同の意味、三角形の合同条件、記号≡を用いた合同の表し方を理解する。1.単元 平行と合同 2.指導観 図形に関する学問としての起源は古代エジプトであるといわれている。ナイル川の氾濫により土 地の測量が必要となり、人々が生活する上での大切なものとして幾何学が生まれた。やがてギリシ



U9j580gf8iba369ji2w Xyz P 970



中学数学単元別 平行と合同 数学 中学校 教材 問題集 4 学林舎 通販 Yahoo ショッピング
1 単元名 平行と合同 2 題材の考察 生徒の実態 -略- 題材について 生徒たちは、図形に関して、小学校で観察や構成などの活動を通して、基本的な平面図形や立体に ついて理解を深めてきた。1 単元名 「平行と合同」 2 単元の目標 観察,操作や実験などの活動を通して,基本的な平面図形の性質を見いだし,平行線の性質を基に して,それらを確かめたり,図形の合同について理解し図形の見方を深めることができるようにす る。平行線や角の性質、それに基づいた図形の性質の理解をもとにして、三角形や多角形などの角の値を求める練習ができる問題プリントです。 中学2年生 数学 合同と証明 練習問題プリント 無料ダウン




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中2数学 平行と合同4 三角形の内角と外角 すべて無料 星組の中学数学講座
平行四辺形は2つの合同な三角形を2つ、対応するひと組の辺を共有し、その両端の頂点が対応と逆順に重なるように並べた図形である。 三角形の面積を 〔底辺〕×〔高さ〕÷2 で表すことができるのは、それが平行四辺形の面積を2等分して求めた結果だから平行な2直線に1つの直線が交わると き、「錯角は等しい」という平行線の性質 を利用します。 合同な図形では、対応する辺の長さ や角の大きさが等しくなります。 平成25年度全国学力・学習状況調査A「6(2)」の問題です。1単元名 平行と合同 2単元の評価規準 知識・技能 思考・判断・表現 主体的に学習に取り組む態度 ・平行線や角の性質を理解すること・数学的な推論の過程に着目し,図・平面図形の性質を見いだそうとし ができる。 形の性質や関係を,平行線や角の ている。



中学数学 三角形の合同の証明 その1 中学数学の無料オンライン学習サイトchu Su



中2数学 合同 三角形の合同条件まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
1 単 元 「平行と合同」(第4章) 2 校内研とのかかわり (1) 数学科研究目標 「自ら学ぶ意欲を育てる指導法の研究」 (2) 数学科としてとらえる「学習意欲」について ・「なぜ?」という思いを抱き,それを解明しようと様々な方法に取り組もうとしている。平行線と角の性質について理解している。 平行線の性質や三角形の性質を基にして,多角形の角についての性質を見いだせる。 平面図形の合同の意味を理解している。 (2)定着への手立て 掲示物で,短時間で基礎的なことを確認する。ともかく、三辺が等しいために合同であるのでしたがって、 ∠adb=∠cbd である。 錯角の角度が等しいので、よって ad//bc ある。 同様にして ab // dc も証明できる。 そして、対辺どうしが平行の四角形であるので、平行四辺形であることが導ける。



中学数学 図形の合同 図形の性質




中2 中2数学 平行と合同2 中学生 数学のノート Clear




中2 平行と合同 平行線と角 中学生 数学のノート Clear



Http Www Edu City Misato Lg Jp Secure 0526syoumei Mondai Pdf




世界一わかりやすい数学問題集中2 4章 平行と合同と証明




中2数学 平行と合同10 1 8 角度の問題 のまとめ すべて無料 星組の中学数学講座




4章 平行と合同 2 多角形の外角の和 Ppt Download



中2数学 平行と合同 写真の図形の問題について質問します Yahoo 知恵袋



平行と合同 ドリるーむ




中2 中2数学 平行と合同2 中学生 数学のノート Clear



Studydoctor三角形の合同の利用 中2数学 Studydoctor



高校入試 英語 数学 学習 平行と合同 図形の合同と証明




合同 算数星人のweb問題集 中学受験算数の問題に挑戦




無料 中2数学 テスト対策 解答プリント 216 図形と合同4 平行四辺形




中2数学 平行と合同18 いろいろな証明 すべて無料 星組の中学数学講座




三角形の合同条件 小学生 中学生の勉強



証明 合同 相似 が苦手な人へ 教遊者




中2 数学 平行と合同 この問題を教えてください 下の図で 同じ印が 数学 教えて Goo



4 図形の調べ方 1章 平行と合同 3 三角形の合同 2時間 Ppt Download



1




中2 中2数学 平行と合同2 中学生 数学のノート Clear




中2 中2数学 平行と合同2 中学生 数学のノート Clear



Www Tsumugi Ne Jp Member Data Sm2 4 Sm2 4 5 Pdf




世界一わかりやすい数学問題集中2 4章 平行と合同と証明




同位角 錯角とは 中2平行と合同2 Youtube




岩手県高校入試対策 数学 平行と合同 図形の性質 09年度第1回白ゆり入試プレテスト 岩手県 高校入試 受験対策 定期テスト対策等の要点整理方法
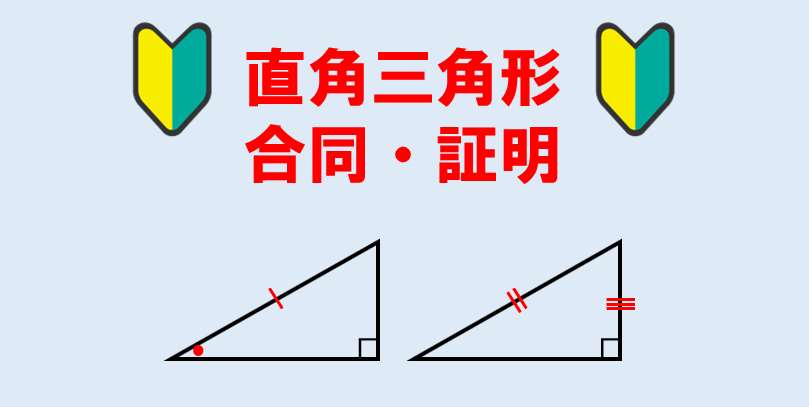



中2数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
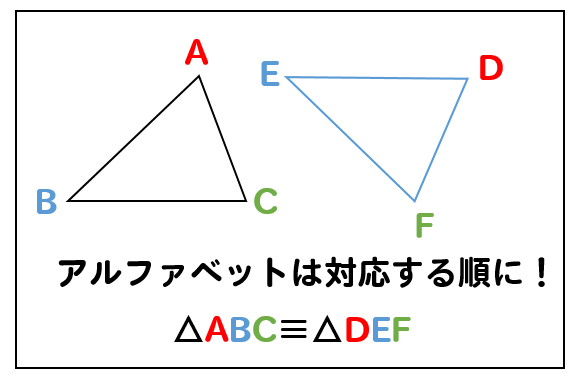



中学数学 合同な図形の性質とは 見つけ方は 問題を使って解説 数スタ




中学2年 平行と合同 の問題 いつも母に教わっているのですが 中学 数学 教えて Goo
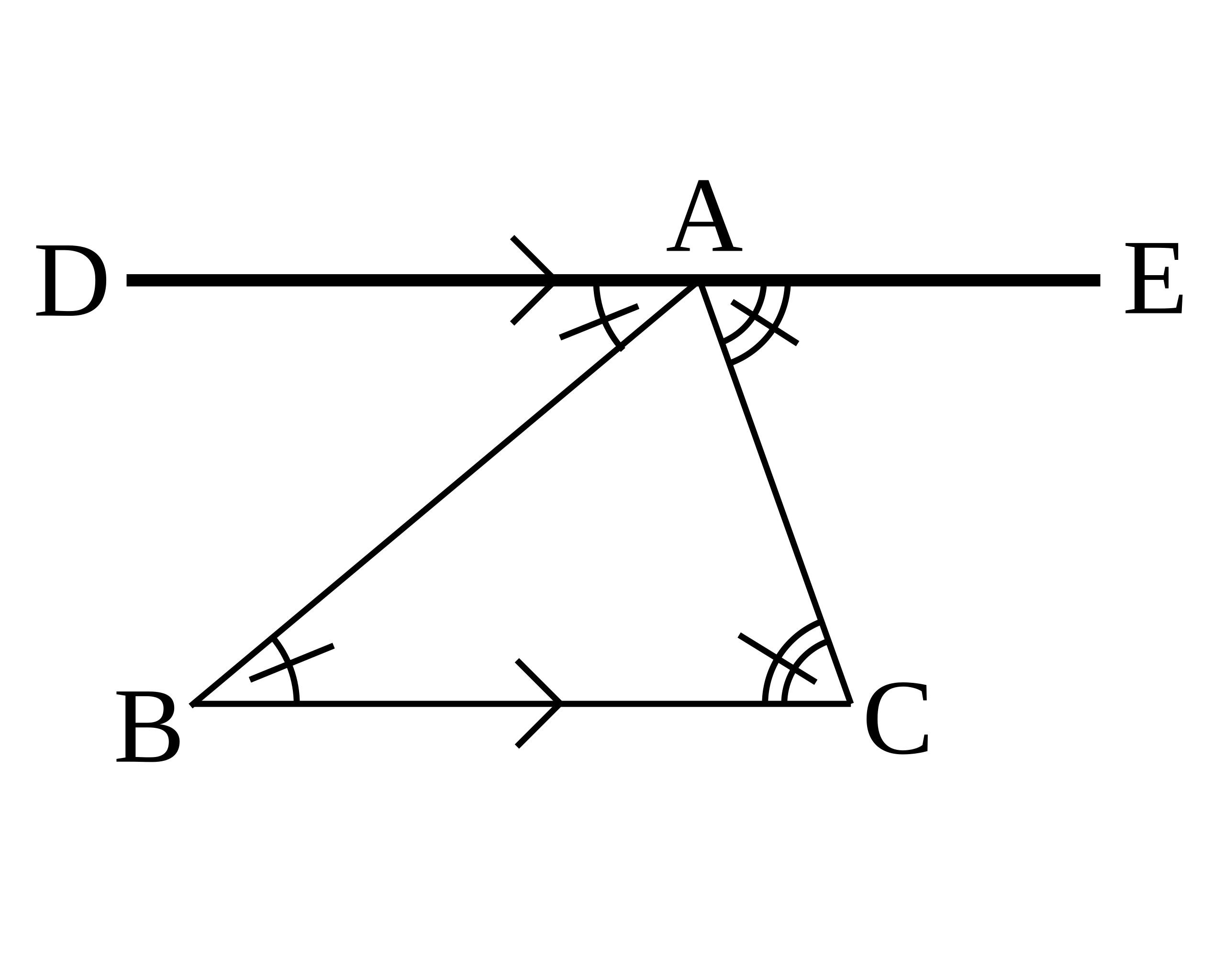



ファイル 平行と合同1 Svg Wikibooks
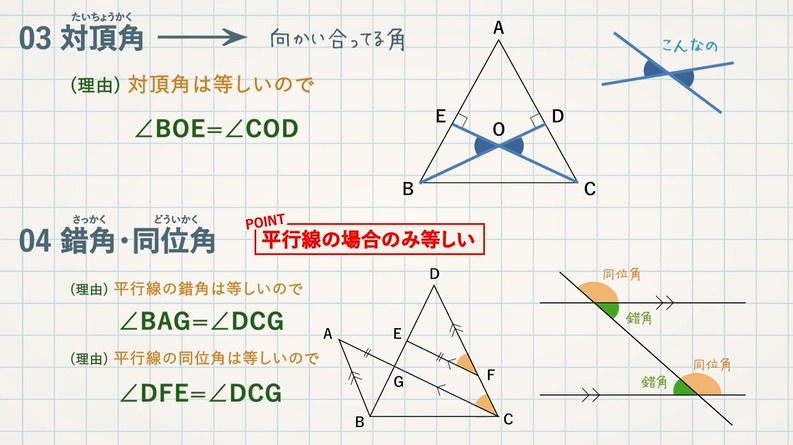



証明 合同 相似 が苦手な人へ 教遊者
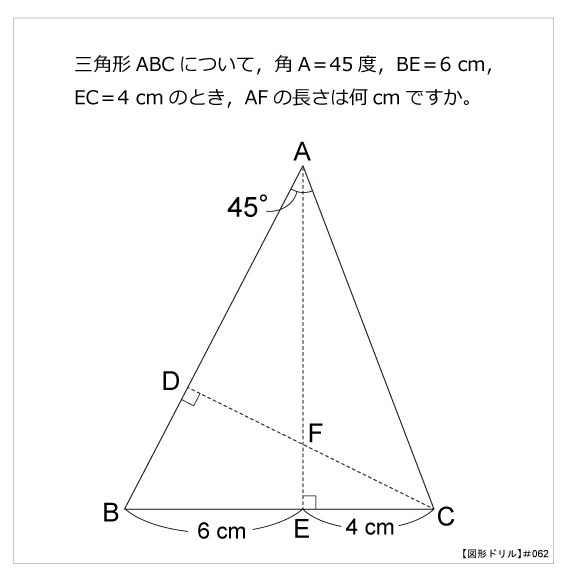



図形ドリル 第62問 合同の発見 算数星人のweb問題集 中学受験算数の問題に挑戦




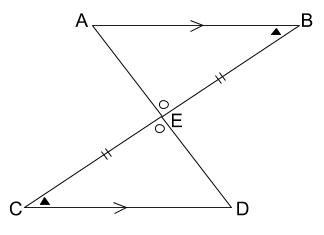
合同の証明2




図形の性質と合同 の勉強法のわからないを5分で解決 映像授業のtry It トライイット



高校入試 英語 数学 学習 平行と合同 平行線と角




中2数学 平行と合同 01 2 対頂角 同位角 錯角 練習問題 Youtube




中学生2年生向け 平行と合同について



平行と合同 ドリるーむ
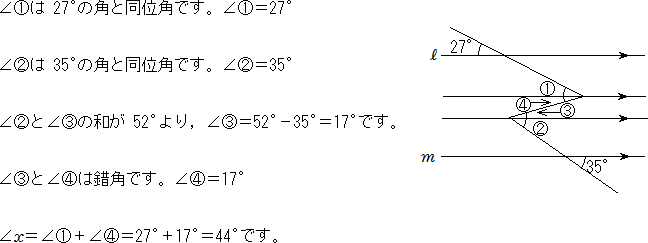



平行と合同 補助線をひいて Xの大きさを求める問題 中学数学 定期テスト対策サイト



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生



三角形の合同条件 思考力を鍛える数学



Q Tbn And9gcskwsqwonbwiahxcrm0ofdcuraehkhkmuzi9rmuiorblbkhbpc7 Usqp Cau



平行と合同 ドリるーむ




数学2年 図形 サンプル 数学中学2年 会員版では高校入試問題を詳細に解説しています 角 三角形 四角形 多角形 角 対頂角 同位角 錯角 問題1 正解1 解説1 問題2 正解2 解説2 問題3 正解3 解説3
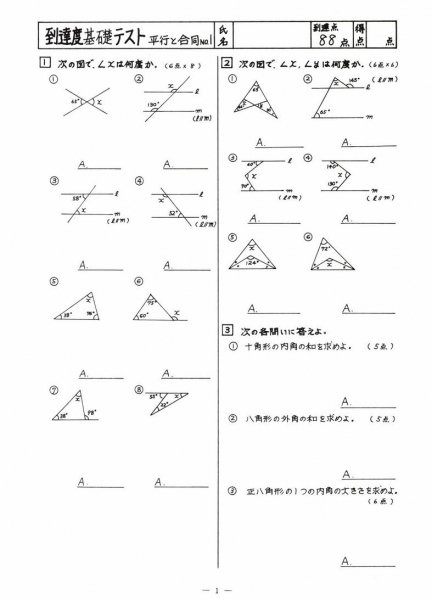



中学数学到達度テスト集シリーズの販売 教材出版 学林舎
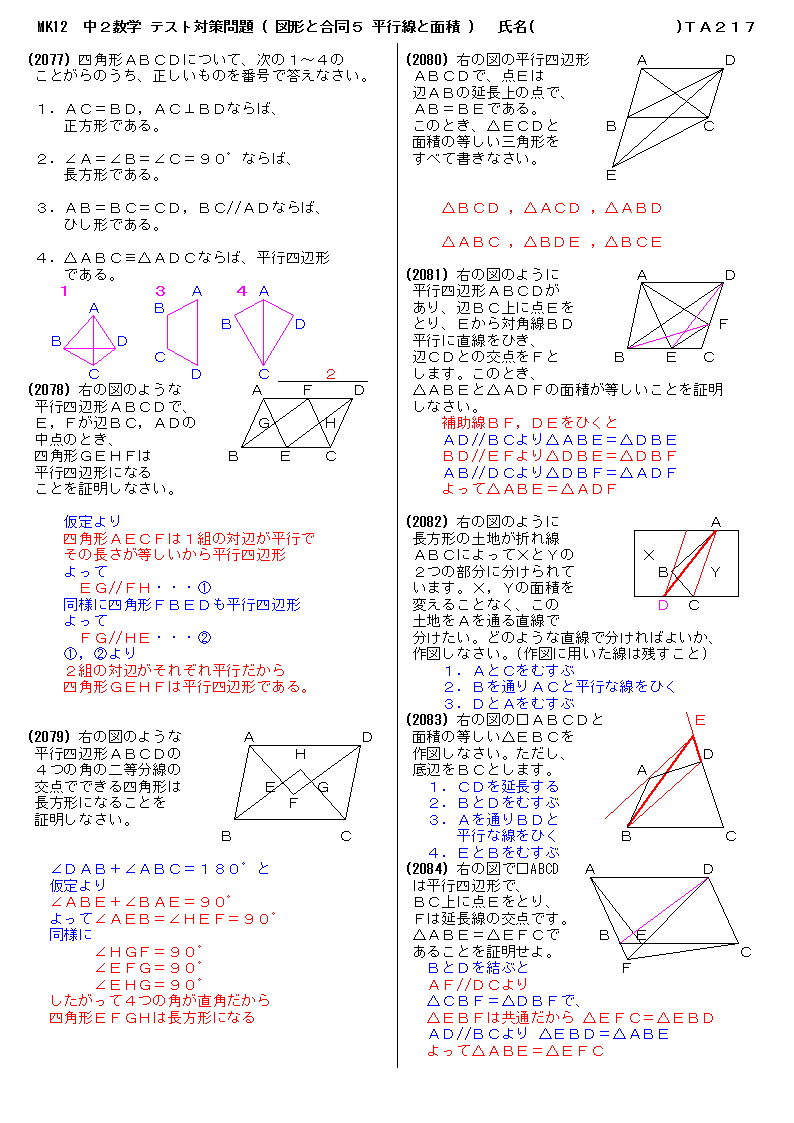



無料 中2数学 テスト対策 解答プリント 217 図形と合同5 平行線と面積



令和3 21 年度用 中学校数学 内容解説資料a
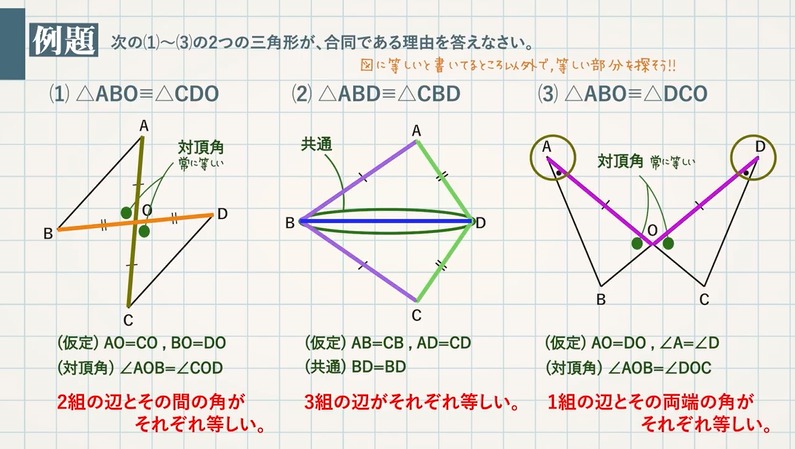



合同な図形とは 三角形の合同条件 教遊者




世界一わかりやすい数学問題集中2 4章 平行と合同と証明
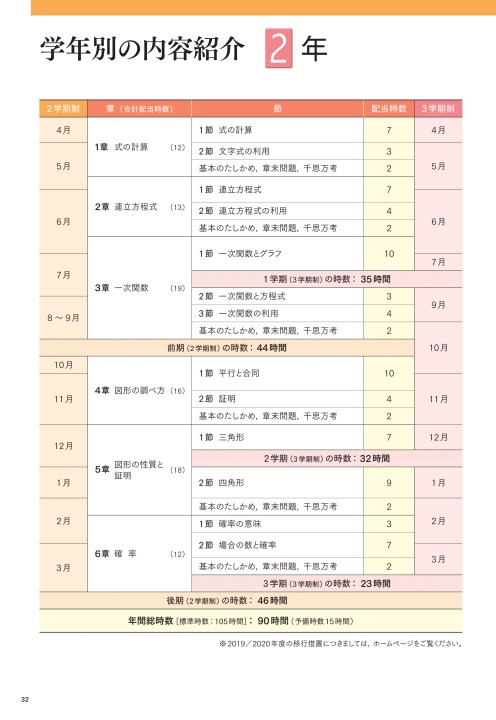



年度用 中学校数学教科書内容解説資料 未来へひろがる数学




中2数学 平行と合同14 三角形の合同条件 すべて無料 星組の中学数学講座
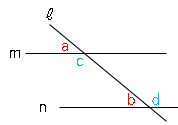



平行と三角形の合同 数学の要点まとめ 練習問題一覧
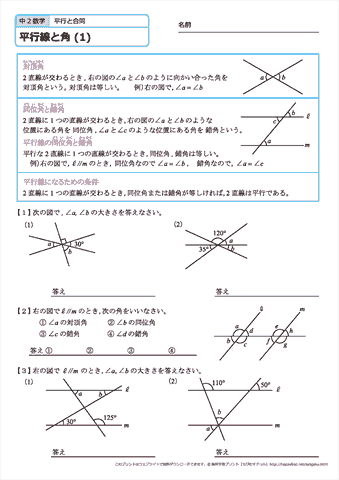



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
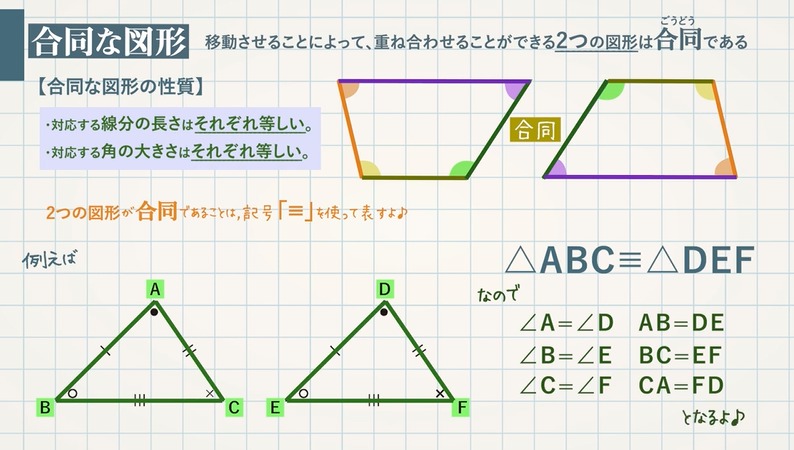



合同な図形とは 三角形の合同条件 教遊者




小テスト無料公開 中2数学 平行線と角 Thai Tutorial Education
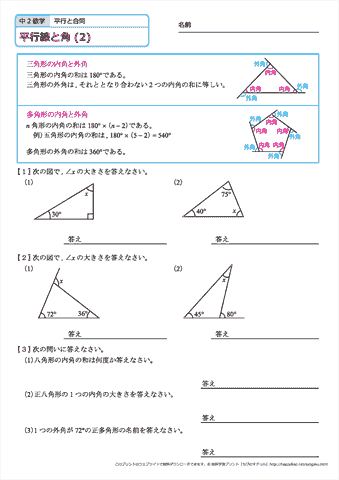



中学2年生 数学 平行線と角 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1



Http Www1 Iwate Ed Jp Kenkyu Siryou H26 H26 0304 2 Pdf
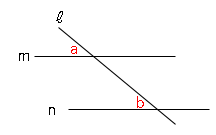



平行と三角形の合同 数学の要点まとめ 練習問題一覧




合同条件と性質について 中2 中3 家庭教師とっしゅ先生の授業 小学生 中学生




世界一わかりやすい数学問題集中2 4章 平行と合同と証明



Math 平行と合同 証明の書き方 2 よく出る問題 働きアリ The 2nd




平行と合同 補助線をひいて Xの大きさを求める問題 中学数学 定期テスト対策サイト




1次関数と合同と高さの比 高校入試 数学 良問 難問



Www Kyoiku Shuppan Co Jp Textbook Chuu Sugaku Docs H28chu Sugaku 26pt Pdf




世界一わかりやすい数学問題集中2 4章 平行と合同と証明



1




世界一わかりやすい数学問題集中2 4章 平行と合同と証明



Math 平行と合同 角の二等分線と角度 働きアリ




ギザギザ角度の求め方は 中2平行と合同6 Youtube



Http Www Center Ibk Ed Jp Action Common Download Main Upload Id 5610



Mathematics 平行と合同 証明の書き方 2 よく出る問題 働きアリ
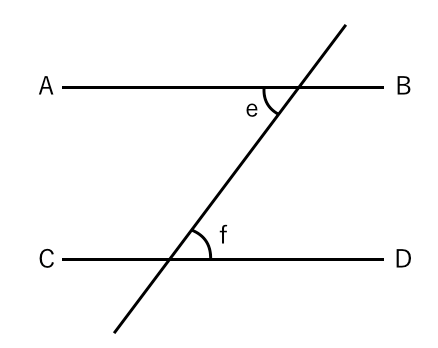



合同な図形 仮定と結論について 苦手な数学を簡単に



至急 中学2年平行と合同 いろいろな角度の求め方 写真の問題の丸をつけている問 Yahoo 知恵袋



中学数学単元別 平行と合同 数学 中学校 教材 問題集 4 学林舎 通販 Yahoo ショッピング




中2 中2数学 平行と合同2 中学生 数学のノート Clear




中2 中2数学 平行と合同1 中学生 数学のノート Clear




岩手県高校入試対策 数学 平行と合同 図形の性質 09年度第1回白ゆり入試プレテスト 岩手県 高校入試 受験対策 定期テスト対策等の要点整理方法
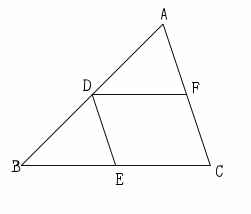



平行線の証明
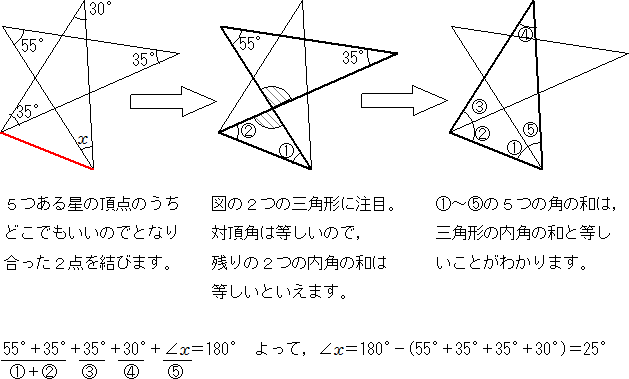



平行と合同 星の形の角度を求める問題 中学数学 定期テスト対策サイト




Math 平行と合同 角の二等分線と角度 働きアリ




スタディピア 図形
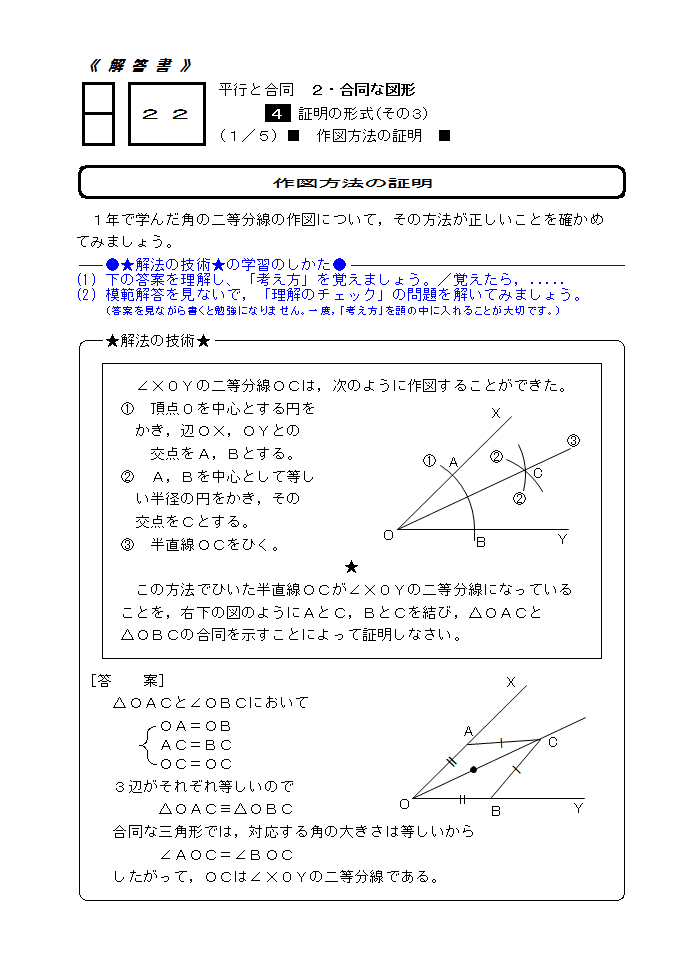



中学数学 きょうの1題 平行と合同 22 中学数学高校数学個別指導in山形市 数専ゼミ




Math 平行と合同 角の二等分線と角度 働きアリ
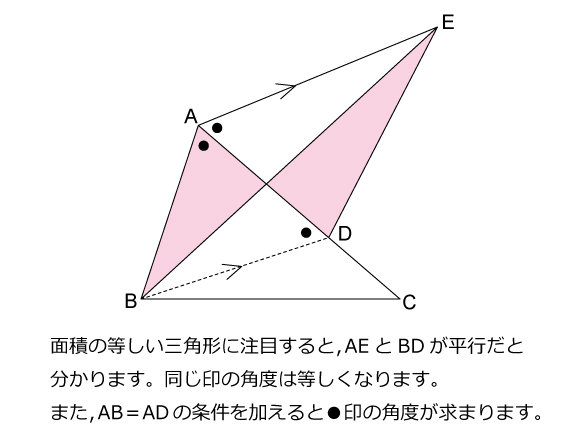



合同な三角形の問題 Faicidy7



平行と合同における内角と外角の定義




中2数学 平行と合同 07 仮定や結論 証明の基礎 解説 練習問題 Youtube



Ten Tokyo Shoseki Co Jp Text Chu Current Sugaku Files Thema Sugaku 09 Pdf



0 件のコメント:
コメントを投稿