Multiplication of Polynomials ?While considering this question; a^2 b^2 = (a – b)^2 2ab (a – b)^2 = a^2 – 2ab b^2 (a b c)^2 = a^2 b^2 c^2 2ab 2ac 2bc (a – b – c)^2 = a^2 b^2 c^2 – 2ab – 2ac 2bc (a b)^3 = a^3 3a^2b 3ab^2 b3 (a b)^3 = a^3 b^3 3ab (a b) (a – b)^3 = a^3 – 3a^2b 3ab^2 – b^3 a^3 – b^3 = (a – b) (a^2 ab b^2)

Find The Value Of A 3 B 3 C 3 3abc If 1 A B C 8 Ab Ca 19 2 A B C 5 A 2 B 2 C 2 11
(a b)^3 formula
(a b)^3 formula-Consider a triangle with sides of length a, b, c, where θ is the measurement of the angle opposite the side of length cThis triangle can be placed on the Cartesian coordinate system aligned with edge a with origin at C, by plotting the components of the 3 points of the triangle as shown in Fig 4 = (, ), = (,), = (,) By the distance formula, = () () a^3 b^3 c^3 a 3 b 3 c 3 = (a b c) (a 2 b 2 c 2 – ab – bc – ca) 3abc s Algebra, cube, sum, sum of cubes This entry was posted on at 554 pm and is filed under Algebra You can follow any responses to this entry through the RSS feed You can leave a response, or trackback from your own site




Prove That A B 3 B C 3 C A 3 3 A B B C C A 2 A 3b 3c 3 3abc Brainly In
For this question, we can use the identity (abc) 2 = a 2 b 2 c 2 2ab abc 2ca (abc) 2 = 250 2 (ab bc ca) (abc) 2 = 250 2 (3) (abc) 2 = 250 6 (abc) 2 = 256 abc = square root of 256 abc = 16 There you go Get the list of basic algebra formulas in Maths at BYJU'S Stay tuned with BYJU'S to get all the important formulas in various chapters like trigonometry, probability and so on 1 Trigonometry Draw a line for the height of the triangle and divide the side perpendicular to it into two parts b = b₁ b₂ From sine and cosine definitions, b₁ might be expressed as a * cos(γ) and b₂ = c * cos(α)Hence b = a * cos(γ) c * cos(α) and by multiplying it by b, we get b² = ab * cos(γ) bc * cos(α) (1) Analogical equations may be derived for other two
Click here👆to get an answer to your question ️ If a^2 b^2 c^2 = 250 and ab bc ca = 3 , then find a b c 41K answers 2M people helped The Formula is given below (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) Explanation Let us just start with (abc)² = a² b² c²2ab2bc2ca =a² b² c²2 (abbcca) nowThe only appropriate response I can think of is how to interpret the exponent Any parentheses raised to the nth power means you have to rewrite that expression n times and then multiply them all In this case the exponent is just 2, so we rewri
= a 2 ab ac ba b 2 bc ca cb c 2 Adding like terms, the final formula (worth remembering) is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac Practice Exercise for Algebra Module on Expansion of (a b c) 2Simplify a b c = 25 and ab bc ca = 59 Find the value of a 2 b 2 c 2 Solution According to the question, a b c = 25 Squaring both the sides, we get (a b c) 2 = (25) 2 a 2 b 2 c 2 2ab 2bc 2ca = 625 a 2 b 2 c 2 2(ab bc ca) = 625 a 2 b 2 c 2 2 × 59 = 625 Given, ab bc ca = 59 a 2 b 2 c 2 118 = 625N Michael could rewrite the expression as 3 and move 3 spaces to the right My find the value a if xa is a factor of x³3x²4xa




Find The Value Of A 3 B 3 C 3 3abc If 1 A B C 8 Ab Ca 19 2 A B C 5 A 2 B 2 C 2 11




Prove That A 2 B 2 C 2 Ab Ca Is Always Non Negative For All Valuesof A B And C Brainly In
Stepbystep explanation = a2 – 2ab b2 Therefore, (a b)2 (a – b)2 = a2 2ab b2 a2 – 2ab b2 = 4abRecall the formula ` (abc)^2 = a^2 b^2 c^2 2 (ab bc ca)` Given that `a^2 b^2 c^2 = 250 , ab bc ca = 3 ` Then we have ` (abc)^2 = a^2 b^2 c^2 2 (ab bcca)` ` (abc)^2 = 250 2 (3)` ` (abc)^2 = 256` ` (abc) =± 16` Ross answered this abc whole cube = a cube b cube c cube 3 (ab) 3 (bc) 3 (ac) Was this answer helpful?




If A 2 B 2 C 2 1 Then Ab Ca Lies In The Interval Youtube




A B 3 B C 3 C A 3 A A B C A 2 B 2 C 2 Ab Ac B 3 A B B C C A C Youtube
RD Sharma Class 9 Solutions Chapter 12 Heron's Formula RD Sharma Class 9 Solution Chapter 12 Heron's Formula Ex 121 Question 1 In the figure, the sides BA and CA have been produced such that BA = AD and CA = AEAbc(1/a 1/b 1/c) = (3)(−2) bc ca ab = −6 Using the a 2 b 2 c 2 formula, a 2 b 2 c 2 = (a b c) 2 2(ab bc ca) a 2 b 2 c 2 = (3) 2 2(6) = 9 12 = 21 Answer a 2 b 2 c 2 = 21 Example 3 Find the value of a 2 b 2 c 2 if a b c = and ab bc ca = 100 Solution To find a 2 b 2 c 2 Given that a b c = ab bc ca = 100Với abc là các số thực dương thỏa mãn ab bc ca = 3abc Tìm giá trị nhỏ nhất của P = Câu hỏi và hướng dẫn giải Nhận biết Với a,b,c là các số thực dương thỏa mãn ab bc ca = 3abc Tìm giá trị nhỏ nhất của P = A P min = 3/2 B




If A B C 6 And Ab Ca 11 Is Given Then Find The Value Of A 3 B 3 C 3 3abc Youtube




Q3 Add The Following I Ab B Lido
Substitute the values of (a 2 b 2 c 2 ) and ( a b c ) in the identity (1), we have (12) 2 = 50 2 ( ab bc ca ) ⇒ 144 = 50 2 ( ab bc ca ) ⇒ 94 = 2 ( ab bc ca) ⇒ ab bc ca = `94/2` ⇒ ab bc ca = 47 Concept Expansion of Formula Report Error What is the formula of a3 b3 c3?#rbclasses9email rbclassesmtr@gmailcomwatsapp number R B Gautam R B Classes9th class Number Systemshttps//wwwyoutubecom/watch?v=PUUrm0qDQ&l



View Question Prove A B 3 B C 3 C A 3 3 A B B C C A



If A B C 5 And Ab Ca 10 Then Prove That A3 C3 3abc 25 Studyrankersonline
a 3 − b 3 = (a − b) (a 2 b 2 ab) a 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3 (a b) (b c) (c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3 = 3abc$$(a b c)^3 = (a^3 b^3 c^3) 3a(ab ac bc) 3b(ab bc ac) 3c(ac bc ab) 3abc$$ $$(a b c)^3 = (a^3 b^3 c^3) 3(a b c)(ab ac bc) 3abc$$ $$(a b c)^3 = (a^3 b^3 c^3) 3(a b c)(ab ac bc) abc$$ It doesn't look like I made careless mistakes, so I'm wondering if the statement asked is correct at all`x x^2 x^3 x^4` Polynomial `7 y 5x` Binomial `2y – 3y^2` Binomial `2y – 3y^2 4y^3` Trinomial `5x – 4y 3xy` Trinomial `4z – 15z^2` Binomial `ab bc cd da` Polynomial `pqr` Mononomial `p^2q pq^2` Binomial `2p 2q` Binomial




Prove That A B 3 B C 3 C A 3 3 A B B C C A 2 A 3b 3c 3 3abc Brainly In




ユニークab Ca 子供のための最高のぬりえ
(abbcca)² = (ab) ²(bc)²(ca)²2(ab)(bc)2(bc)(ca)2(ca)(ab) hence, (ab)²(bc)²(ca)²2ab²c2abc²2a²bc (ab)²(bc)²(ca)²2abc(bca)2 b 2 c 2 ab bc ca as Sum of Squares Here we will express a 2 b 2 c 2 – ab – bc – ca as sum of squares a 2 b 2 c 2 – ab – bc – ca = 1 2 {2a 2 2b 2 2c 2 – 2ab – 2bc – 2ca} = 1 2 { (a 2 b 2 – 2ab) (b 2 c 2 – 2bc) (c 2 a 2 – 2ca)}Given a b c = 9 a 3 b 3 c 3 – 3abc = 27 Formula Used a 3 b 3 c 3 – 3abc = (a b c)(a 2 b 2 c 2 – ab – bc – ca) (a b c) 2 = a 2




Prove That The Determinant Is A B B C C A A 2 B 2 C 2 Mathematics Stack Exchange




Math 9 Flip Book Pages 101 150 Pubhtml5
on the number line, which step could Michael complete to evaluate the expression?Example Solve 8a 3 27b 3 125c 3 30abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 30abc) can be written as (2a) 3 (3b) 3 (5c) 3 (2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 Given #v= 2(ab bc ca)#, how do you solve for a?




Prove That A B C 3 A 3 B 3 C 3 3 A B B C C A Youtube
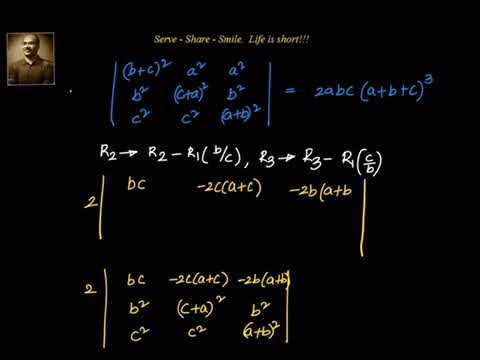



Matrices Determinants Prove Det 2abc A B C 3 Youtube
The area of whole square is ( a b c) 2 geometrically The whole square is split as three squares and six rectangles So, the area of whole square is equal to the sum of the areas of three squares and six rectangles ( a b c) 2 = a 2 a b c a a b b 2 b c c a b c c 2 Now, simplify the expansion of the a b c wholeA3 b3 =(ab)−3ab(a b) 5 (a−b)3 = a3 −b3 −3ab(a−b);4 Mahi C Patel, added an answer, on 6/6/19 Mahi C Patel answered this ( a b c ) 3 = ( a b c ) ( a2 b2 c2 ab bc ca ) 3 abc We transferred the 3 abc to the other side as we required



If A B C Ab Ca 0 Then How Can You Prove That A B C 3abc Quora




Algebraic Formulas Part 1 Math Methods Studying Math Math Formula Chart
12d 2 (abacaebcbece) 12e 2 (abacadbcbdcd) We can choose x 2 as above in 6 ways From the remaining 2 factors, we can choose two different letters in C(2,1)⋅C(1,1) ways, giving in all 12 ways We can choose 1 letter from 5 in 5 ways And 2 letters from 4 in C(4,2) ways giving 30 ways The sum of the coefficients is therefore 30⋅Solution for abbcca=abc equation Simplifying ab bc ca = abc Reorder the terms ab ac bc = abc Solving ab ac bc = abc Solving for variable 'a' Move all terms containing a to the left, all other terms to the rightSum Of Cubes Formula A – 3Ab (A – B) A3 C3– 3Abc = (A B C)( B2 C2 – Ab – – Ca) What Is The Cube Formula?




Prove A3 C3 3abc A B C B2 C2 Ab Ac Youtube




A 3 B 3 C 3 Formula Brainly In
(a3 b3 c3 – 3abc) = (a b c)*(a2 b2 c2 – ab – bc – ac) 13 How do you expand a b3?Algebra Linear Equations Formulas for Problem Solving 1 Answer P dilip_k What is the perimeter of the rectangle if the area of a rectangle is given by the formula How do you find the value of y that makes (3,y) a solution to the equation #3xy=4#?b2 =(ab)2−2ab 2 (a−b)2 = a 2−2ab b;




B2 C2 Ab Ca Formula Love Meme




B2 C2 Ab Ca Formula Love Meme
I simplified this equation too $$(ab)^3(bc)^3(ca)^3=abc(a^3b^3c^3)$$ I tried to subtract $3(abc)^2$ from both sides and it gave a factorised form $$(abbcca)((ab)^2(bc)^2(ca)^2abc(abc))=abc(abc)(a^2b^2c^2abbcca)$$ How can I proceed after that?A3 −b3 =(a−b)33ab(a−b) 6 a2 −b2 =(ab)(a−b) 7 a3 −b3 =(a−b)(a2 ab b2) 8 a3 b3 =(ab)(a2 −ab b2) 9 a n−bn=(a−b)(an−1 a −2b an−3b2Ab, V bc, and V ca (or phase voltages) into two symmetrical componentsV p andV n (of the line or phase voltages) The two balanced components are given by V VaV aV p = ab bc ca ⋅ ⋅2 3 (4) V VaV aV n = ab bc ca ⋅ ⋅2 3 (5) where aa=∠ ° =∠ °1 1 1 240and 2 The positive and negative sequence voltages can be used when ana



93vcqcm F14asm




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf
Example Solve 8a 3 27b 3 125c 3 – 90abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3(2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3first of them is equal to (ab c)2 −2(ab bcca) So the instances of equality are described by the system of two equations ab c = 1, abbc ca = 0 plus the constraint a,b,c 6= 1 Elimination of c leads to a2 abb2 = ab, which we regard as a quadratic equation in b,b2 =(a−b)22ab 3 (a b c)2 = a2 b2 c2 2(ab bc ca) 4 (a b) 3= a3 b3 3ab(a b);




If A B C Is Equals To 6 And A B Ca Is Equals To 11 Find A Cube Plus B Cube Plus C Cube Brainly In




0以上 Ab Ca Formula シモネタ
The Cube Is A Threedimensional Structure Which Is Formed When Six Identical Squares Bind To Each Other In An Enclosed Form A Cube Generally Has 6 Faces, 12 Edges, And 8 VerticesVolume = (1/3)Π r²h L ² = r ² h² sphere Curved surface area = 4Π r² Volume = (4/3)Π r³ Hemisphere Curved surface area = 2Π r² Total Curved surface area=3Π r² Volume = (2/3)Π r³ Cuboid Curved surface area=4h(lb) Total surface area = 2(lbbhh l) Volume = l x b x h Cube Curved surface area=4a ² Total surface area = 6a² Volume = a ³How to multiply Constant and Variable ?




Formula A B C A 2 B 2 C 2 Ab Ca A 3 B 3 C 3 3abc And Problems On It Urdu Hindi Youtube




The Value Of A 3 B 3 C 3 3abc Ab Ca A 2 B 2 C 2 Is Where A 5 B 6 C 10
1 (a b)2 = a2 2ab b2; (abc)^2 >hoac=3(abbcca) giup minh moi minh dang can gap Theo dõi Vi phạm YOMEDIA Trả lời (1) (abc) 2 \(\ge\) 3(abbcca) (*) =>a 2 b 2 c 2 2ab2bc2ca \(\ge\) 3ab3bc3ca =>a 2 b 2 c 2 \(\ge\) abbcca nhân 2 vào cho 2 vế ta được 2a 2 2b 2 NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Exercise 91 Ex 91 Class 8 Maths Question 1 Identify the terms, their coefficients for each of the following expressions (i) 5xyz 2 – 3zy (ii) 1 x x 2 (iii) 4x 2 y 2 – 4x 2 y 2 z 2 z 2 (iv) 3




How To Prove Math A 2 B 2 C 2 Ab Ca Math Is Non Negative For All Values Of Math A B Math And Math C Quora



2
It is a special identity of polynomial of class 9In this video I am going to show you the proof of a3b3c33abc=(abc)(a2b2c2abbcac) I am going to prAnswer Given, a2 b2 c2 −ab−bc−ca multiply and divide by 2 = 22 ×(a2 b2 c2 −ab−bc−ca) = 2a2 −2abb2 b2 −2bcc2 c2 −2aca2Given a b c = 9 ab bc ca = 26 a3 b3 = 91, b3 c3 = 72 and c3 a3 = 35, Formula Used a3 b3 c3 Q19 The distance between points P and Q is 485 km If a person starts from point P with the speed of 60 km/h and another person is running with a certain speed from point Q and they both meet after 25 hours then find the speed of the person who starts from point Q




If A B C 9 And Ab Ca 26 Find A B C Brainly In



2
\(=> (abc)^3 = (a^3ab^2ac^2 2a^2b 2abc 2ca^2)\\ (a^2bb^3bc^2 2ab^2 2b^2c 2abc)\\ (ca^2 cb^2 c^3 2abc 2bc^2 2c^2a) \) Arrage value according power and similear \(=> (abc)^3 = a^3 b^3 c^3 \\ 6abc 3a^2b 3ab^2 \\ 3ac^2 3bc^2 3b^2c 3a^2c \)Quite unfortunately not from the simple perspective requested, I have found that P = a 3 b 3 c 3 3abc = 2S, where S is the area of the triangle of vertices Ex 91, 3 Add the following (i) ab − bc, bc − ca, ca − ab Expressions are ab − bc bc − ca ca − ab We put like terms below like terms So, required sum = 0




What Are Various Forms To Write A B C A Whole Cube Quora
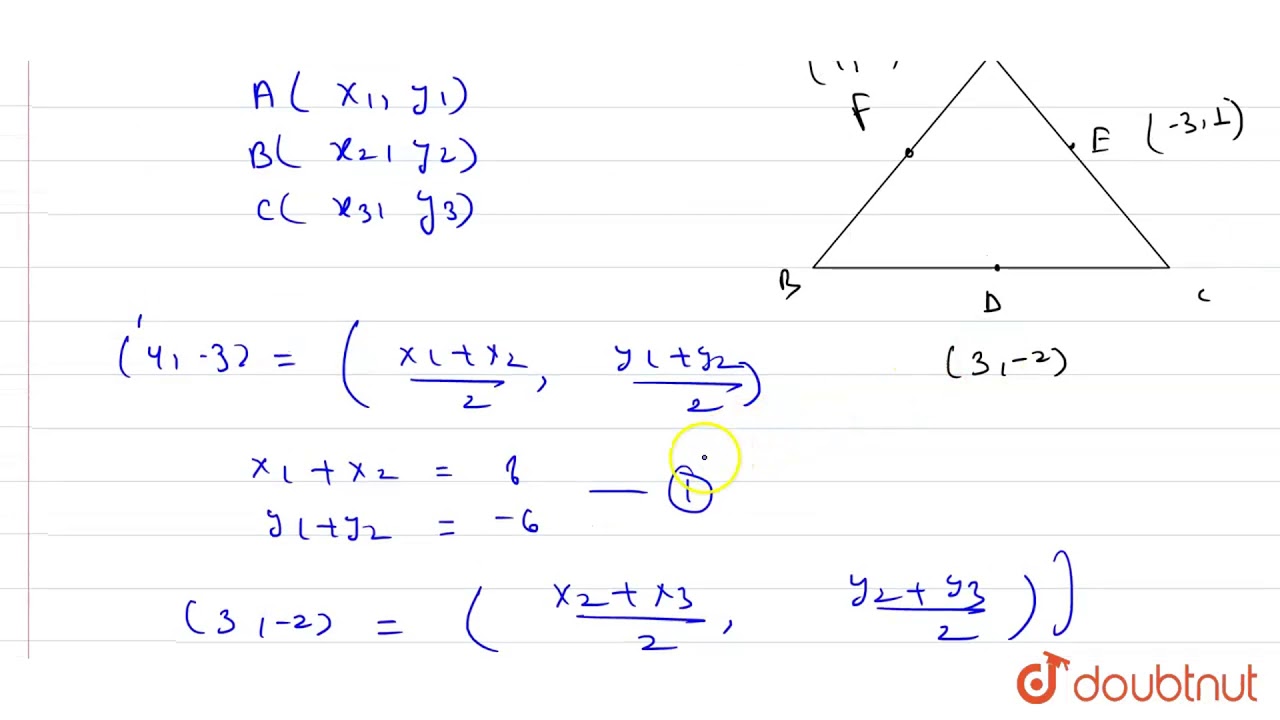



Let D 3 2 E 3 1 And F 4 3 Be The Midpoints Of The Sides Ca Youtube
A 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Before you understand (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ca, you are advised to read How to multiply Variables ?




I Found K A B B C C A But What Is The Chegg Com




What Are Various Forms To Write A B C A Whole Cube Quora




If A B C 2 Ab Ca 1 And Abc 1 And Abc 2 Find The Value Of A 3 B 3 C 3




A 3 B 3 C 3 3abc Formula A B 2 A 2 B 2 2ab Proof Derivation Of Algebraic Identities Youtube Youtube




Using Properties Of Determinants Prove That A B C A B B C C A A 3 B 3 C 3 3abc B C C A A B Mathematics Topperlearning Com Dteg67ff




If A B B C Then Prove That Abc A B C 3 Ab Ca 3 1 Youtube




Factorize 3 A B B C C A Identity A3 C3 3abc Pls Help Me This Brainly In




Misc 13 Using Determinants 3 A B C Ab Ac




What Are Various Forms To Write A B C A Whole Cube Quora




If A B C 3 Abc 12 And Ab Ca 4 Find A3 C3 Brainly In




Prove A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2




If A B C 2 Ab Ca 3 And Abc 4 Then Find The Value Of A B C Brainly In




What Is The Expansion Of A B C 3 Quora




Xz X X Y Y Or Yx Y B2 C2 43 And Ab Ca 3 Gauthmath
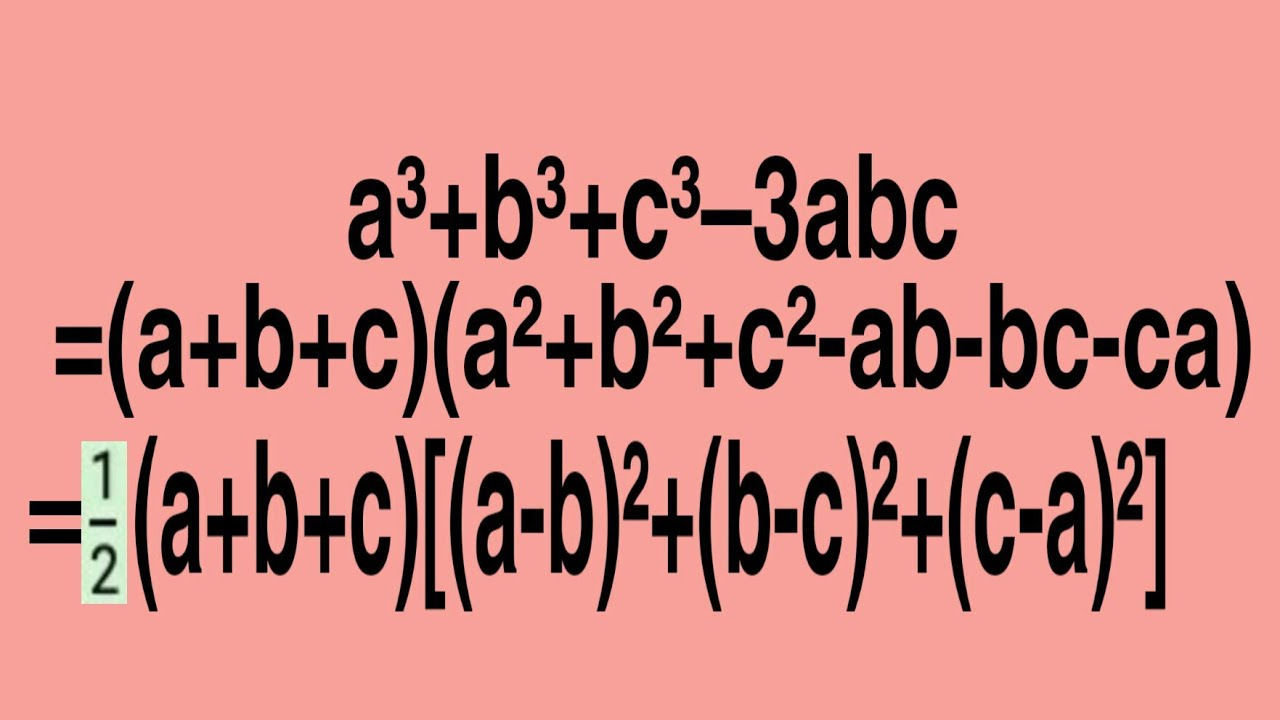



A B C 3abc A B C A B C Ab Ca 1 2 A B C A B B C C A Youtube



If Math A B C 1 Math Math A 2 B 2 C 2 2 Math And Math A 3 B 3 C 3 3 Math Then What Is Math A Times B Times C Math Quora




Add The Following I Ab B Ca Ca Ab Ii A B Ab B C A C A Ac Iii 2p 2q 2 3pq 4 5 Youtube



Abc Is A Triangle With Points D E And F Placed On Sides Ac And Ab Respectively Such That Af Fb 1 1 Dc 1 2 And Ce Ea 1 3 If The




If A B C 9 And Ab Ca 26 Find The Value Of A 2 B 2 C 2 Youtube
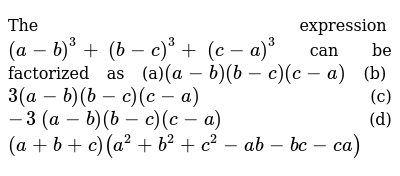



The Expression A B 3 B C 3 C A 3 Can Be Factorized As A A B B C C A B 3 A B B C C A C 3 A B B C C A D A B C A 2 B 2 C 2 A B B C C A




If A B C 9 And Ab Ca 26 Find The Value Of A 3 B 3 C 3 3abc Polynomials Class 9 Maths Youtube




If A B C 11 And Ab Ca Then Find Se C3 3abc Brainly In




Q3 Add The Following I Ab B Lido



If Math A 3 B 3 C 3 3abc Math Then Find The Value Of Math A B C Math Where A B C Quora




Quadratic Equation Session1 Ppt Video Online Download




Factorise A B Whole Cube B C Whole Cube C A Whole Brainly In




Factorise A B B C C A Brainly In




If A B C 5 And Ab Ca 10 Prove A 3 B 3 C 3 3abc 25 Cbse Class 9 Maths Learn Cbse Forum




Xz X X Y Y Or Yx Y B2 C2 43 And Ab Ca 3 Gauthmath




Ab Ca Does Not Exceed Cc




ユニークab Ca 子供のための最高のぬりえ



In A Triangle Abc If Ac Is 15 And Tan C 4 3 Then What Is The Value Of Ab And Quora




What Are Various Forms To Write A B C A Whole Cube Quora




B2 C2 Ab Ca Formula Love Meme




If A B C 0 Then A 3 B 3 C 3 0 How Quora




A Square Plus B Square Plus C Square Formula Examples A 2 B 2 C 2 Formula




Misc 13 Using Determinants 3 A B C Ab Ac



Ooovhspyeiv Im




ユニークab Ca 子供のための最高のぬりえ




Find The Value Of A 3 B 3 C 3 3abc If 1 A B C 8 Ab Ca 19 2 A B C 5 A 2 B 2 C 2 1 Youtube



Search Q A B Whole Cube Tbm Isch



What Is The Value Of A B C 3 Quora




Misc 13 Using Determinants 3 A B C Ab Ac



What Is The Formula Of A B C 2 Quora



コレクション 2ab Ca Formula シモネタ




The Equations Of The Sides Ab Ca Of A Triangle Abc Are 2x Y 0 X Py Q And X Y 3 Respectively And If The Centroid Is 2 3 Then A




What Are Various Forms To Write A B C A Whole Cube Quora




If A Square Bsquare C Square 250 And Ab Ca 3 Find A B C Brainly In
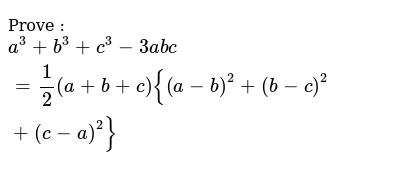



Prove A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2



If The Mid Points Of The Sides Ab Ca Of A Triangle Are 1 5 1 0 4 2 2 3 4 Respectively Then The Length Of The Median From C To Ab Is What Quora




The Sides Ab Ca Of A Triangle Abc Have 3 4 And 5 Points Triangles That Can Be Constructed By Using These Points As Vertices Is




The Following Theorem Has Been Attributed To Chegg Com




2 5 Proving Statements About Segments Ppt Video Online Download



Boolean Expressions 1 Digital Design Analog Design Turnkey Asic Soc Embedded Firmware




If A3 C3 3abc 1 2 A B C A B 2 B C 2 C A 2 Brainly In



How Do You Factor A B C Ab Ca Abc Socratic



If A B C 7 And Ab Ca Find The Value Of A 2 B 2 C 2 Polynomials Maths Class 9



Search Q A 5e3 2bb 5e3 2bc 5e3 Formula Tbm Isch




Q12 If A 2 B 2 C 2 Ab Ca 0 Thena A B C B B C A C C A B D A B C
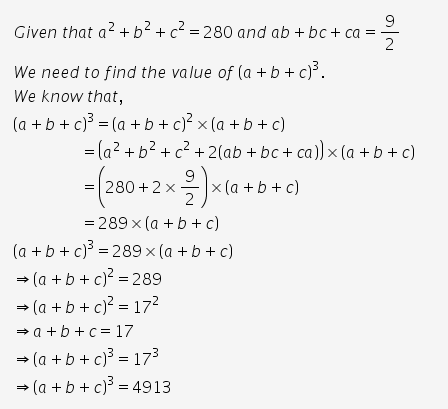



If B2 C2 280 And Ab Ca 9 2 Find The Value Of A B C 3 Cbse Class 9 Learn Cbse Forum
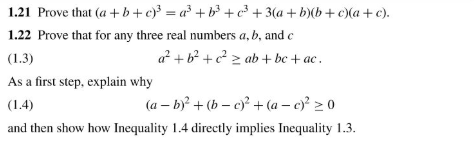



1 21 Prove That A B C 3 A3 C3 3 A Chegg Com




If A B C 0 Then A 2 B C B 2 C A C 2 A B A 0 B 1 C 1 D 3 Youtube




コレクション 2ab Ca Formula シモネタ




Show That Ab Ca Lies In 1 2 1 If Square A Square B Square C 1 Youtube



If A B C 9 And B2 C2 35 Then Find A3 C3 3abc Polynomials Maths Class 9



A 3 B 3 C 3 3abc




A B 2 B C C A B C 2 A B C A C A 2 A B B C Brainly In




If A 2 B 2 C 2 250 And Ab Ca 3 Then Find A B C




ユニークab Ca 子供のための最高のぬりえ



Q Tbn And9gctrh1ypujwtooh8c3vpasyfikri1qchje80vre Ccrxfnsx8i 7 Usqp Cau




Find The Value Of A3 C3 3abc If A B C 15 And Ab Ca 74 Brainly In



If B2 C2 Ab Ca 0 Prove That A B C Polynomials Maths Class 9



0 件のコメント:
コメントを投稿