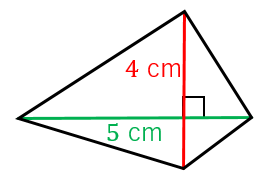
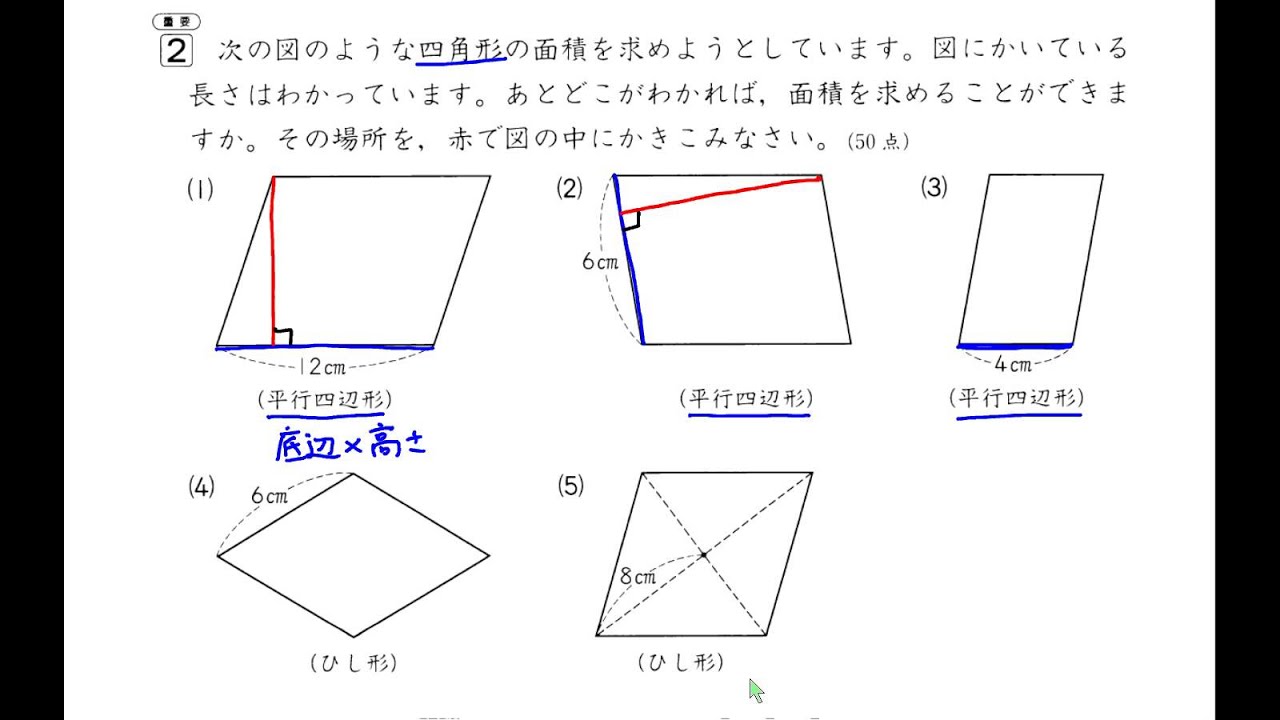
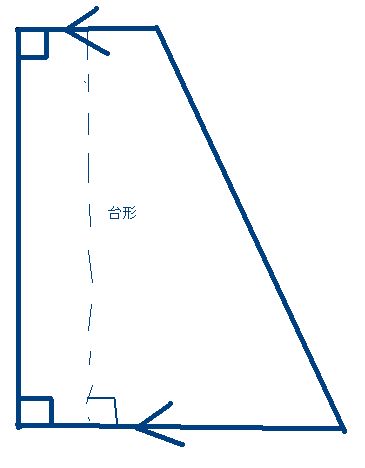
5 四角形の面積を求める ことができる。 三角形の面積の求め方をもと に、四角形の面積を求める。 (考)(技)四角形を 三角形に分割する 考え方を用いて、四 角形の求積ができ る。 6 平行四辺形の面積を求 めることができる。 次の図形は四角形になるんだけど、三角形の面積を利用して解いていきます。 次の四角形の面積を求めましょう。 このような四角形の場合 2つの三角形に分けて考えていきましょう。 上の緑三角形は底辺が5㎝、高さが4㎝だから $$5\times 4\div2=10(cm^2)$$ 下の黄三角形は底辺が5㎝、高さが2㎝だ4つの角のうち2つが直角である四角形を,「2直角四角形」と名付けることにします。 「2直角四角形」の面積を求める問題は,入試でもよく出題されます。 面積を求めるときには,補助線を1本だけ引いて,三角形2つに分けて求めます。 補助線の引き方は,ごく簡単なルールなので,だれでも必ず得意になります。 では,右の図の影の部分の面積を求める問題を例

高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月
四角形の面積 4辺の長さ
四角形の面積 4辺の長さ- 対角線の長さとなす角で表された四角形の面積公式 S=1/2pqsinθ(裏技)の証明、対角線の長さの和が一定である四角形の面積の最大 対角線の長さとなす角で表された四角形の面積公式 S=1/2pqsinθ(裏技)の証明、対角線の長さの和が一定である四角形の面積の最大 スポンサーリンク 高校数学Ⅰ 三角形や四角形、多角形を求積しようとする。 5 単元計画(全13時間) 段階 ねらい 学習活動と内容 配時 気 付 く 〇 長方形を基にして直角三角 形の面積を求めることを通し て、既習の図形に変形すれば 面積を求めることができると




4辺が与えられたとき 面積最大になる四角形は 身勝手な主張
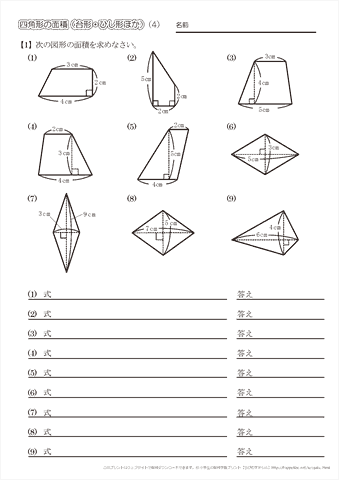
小学5年生の算数 四角形の面積 台形・ひし形ほか 問題プリント 小学5年生の算数 四角形の面積台形・ひし形ほかの問題プリントを無料ダウンロード・印刷 円に外接する四角形の面積 性質2 円に外接する四角形 A B C D ABCD A BC D について,面積は a b c d sin θ 1 θ 2 2 \sqrt{abcd}\sin\dfrac{\theta_1\theta_2}{2} ab c d sin 2 θ 1 θ 2四角形の2本の対角線の長さを$a,b$ 対角線の交わる角度を$\theta$ としたとき、四角形の面積$S$は、 $ S=\displaystyle \frac{1}{2}ab\sin\theta$ 式B である。
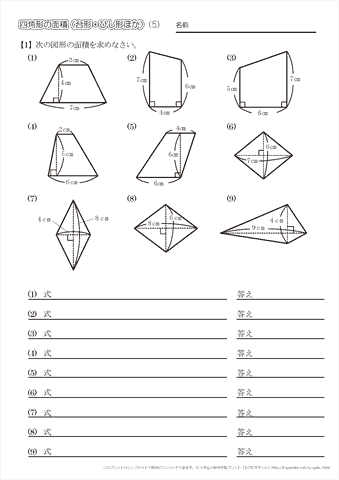
右の図の三角形ABCの面積は48cm 2 です。 四角形DBCEの面積は何cm 2 ですか。 解説 右の図のように、DCを結ぶ。 三角形DBCの面積は 三角形ADCの面積は48× 1 3 =16cm 2 。 三角形ADCの面積は4816=32cm 2 。 三角形ADCの面積は32× 2 3 =21 1 3 cm 2 。 四角形DBCEの面積は16+21 1 3 =37 1 3 cm 2 。 解答 37 1台形やひし形などの公式とその考え方を確認し、四角形の面積を求める練習を繰り返し行うことができます。 四角形の面積/台形・ひし形ほか (1) 答え 四角形の面積/台形・ひし形ほか (2) 答え 四角形の面積/台形・ひし形ほか (3) 答え 四角形の面積/台形・ひし形ほか (4) 答え・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。 ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。
正方形=1辺×1辺=対角線×対角線÷2 平行四辺形=底辺×高さ 台形=(上底+下底)×高さ÷2 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 三角形=底辺×高さ÷2 円の面積の求め方 円の面積=半径×半径×円周率(314) おうぎ形の面積の求め方今回のテーマは、面積が最大の四角形を見つけることです。 高校生以上向きです。 新潟県 タカ3 さんからの追加問題。 問題1 周長一定の三角形のうち、面積が最大になるのは正三角形である事を証明せよ。 問題2 与えられた円に外接する三角形で、面積が最小になるのは正三角形で円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 1辺フラット 円
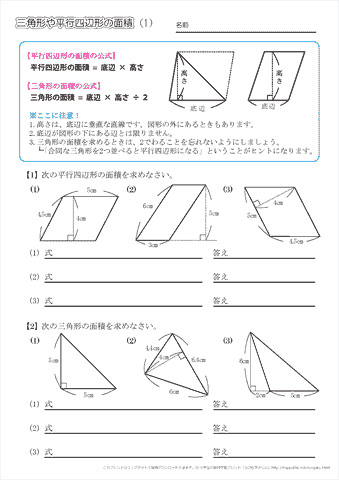



小学5年生の算数 三角形や平行四辺形の面積 問題プリント ちびむすドリル 小学生




小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生
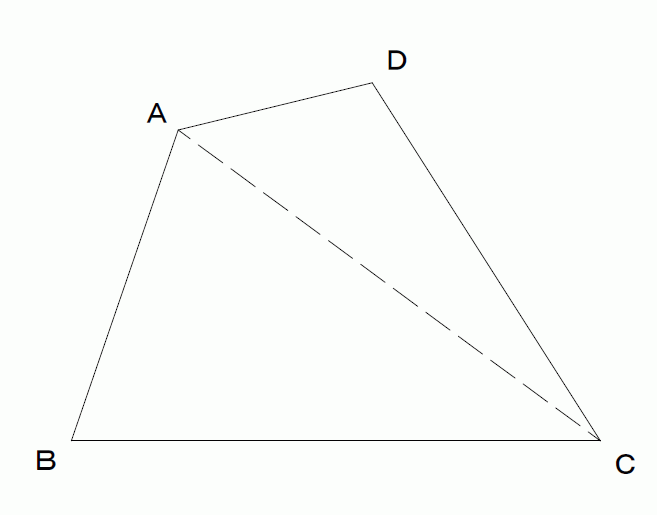
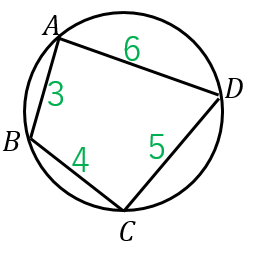
四角形の面積の計算順を守るべき理由 小学校で四角形の面積の求め方は「縦*横」と習います。 そして当然ですがこの計算結果は、順序を「横*縦」に逆転させても同じになります。 縦3cm横5cmの長方形だった場合、以下のようになります。 縦×横:3 * 5 = 15 05314×1=314 314×2=628 314×3=942 314×4=1256 314×5=157 314×6=14 314×7=2198 314×8=2512 314×9=26 四角形ABCDの面積は、2つの三角形の面積を求めて足せば求めることができる。 辺ABの長さは、62=4cm 辺ADの長さは、62=4cm よって三角形ABDの面積は、 4×4÷2=8㎠ 辺BCの長さは、116=5cm 辺CDの長さは、107=3cm よって三角形BCDの面積は、 5×3÷2=75㎠ 四角形ABCDの面積は




小4の算数 四角形の面積と周りの長さの関係 Youtube




高校数学 対角線の長さとなす角で表された四角形の面積公式 S 1 2pqsin8 裏技 の証明 対角線の長さの和が一定である四角形の面積の最大 受験の月
考四角形の面積を2つの三角 形に分割して考え,言葉や 図,式を使って書き表すこと ができる。 表四角形を三角形に分割する 考え方を用いて面積を求め ることができる。 2 平 行 四 辺 形 の 面 5 / 12 ・三角形の面積の求め方や等積変形を「 四角形の面積 」 一覧 正方形・長方形 面積問題④ 小学4年生 計算無料プリント 算数問題 小学生で学習する正方形・長方形 面積 問題です。四角形の面積(「ヘロンの公式」応用) 作者 darkn さん 実行数 5192 一対の対角(の和)が判っていれば,ブレートシュナイダーの公式(Bretschneider's formula) が使えますが,ここでは「長さ情報」のみを使用しています. 辺ABの長さ
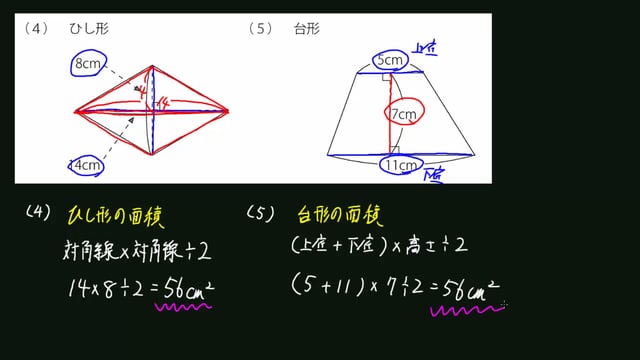



動画解説 みんなの算数オンライン 覚えておこう 四角形の面積の求め方
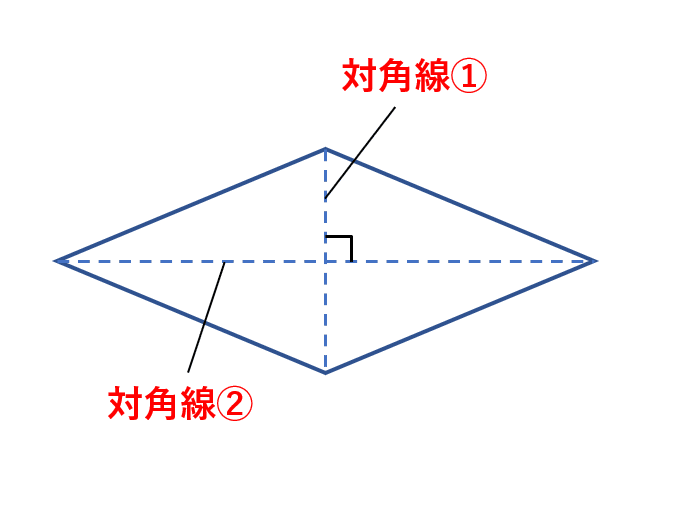



小学算数の面積の求め方と公式一覧 四角形 長方形の性質や円の計算方法まで解説 学びtimes
abeは四角形abcdと面積が等しい三角形だということがわかります。 五角形から三角形への等積変形の作図 下の図の五角形abcdeと面積が等しい afgをつくりなさい。ただし、点f、gは直線cd上にあり、点fはcの左側、点gはdの右側にあるようにしなさい。 対角線acとadをひいて それぞれに平行な線を頂点を通る直線で三角形の面積を二等分する p q r 頂点とその対辺の中点を通る直線は三角形の面積を二等分する。 中点を求める ≫ 2点から直線の式を出す ≫ 図でa(8,8),b(12,0)である。 x y a b o (1)点oを通り aobの面積を二等分する直線の式を求めよ。 (2)点bを通り aobの面積を二等分する直線の式を$3$ 辺の長さと面積がすべて整数であるような三角形を「ヘロンの三角形」(Heronian triangle)と呼ぶ「ピタゴラスの三角形」(各辺の長さがすべて整数であるような直角三角形)は「ヘロンの三角形」であるよって, $1$ 組の辺の長さが等しい $2$ つの「ピタゴラスの三角形」の等辺を貼り合わせたり



対角線と四角形の面積 図形と計量 おおぞらラボ
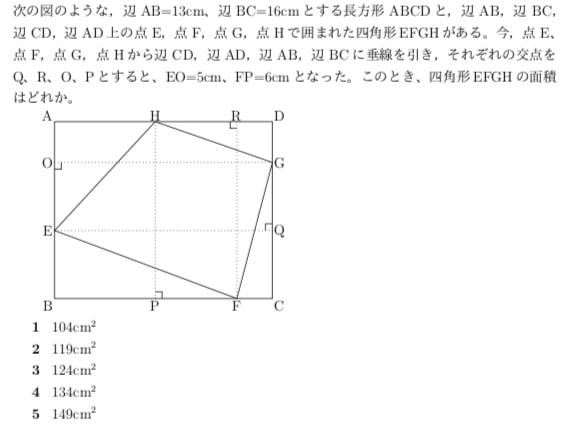



四角形の面積 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
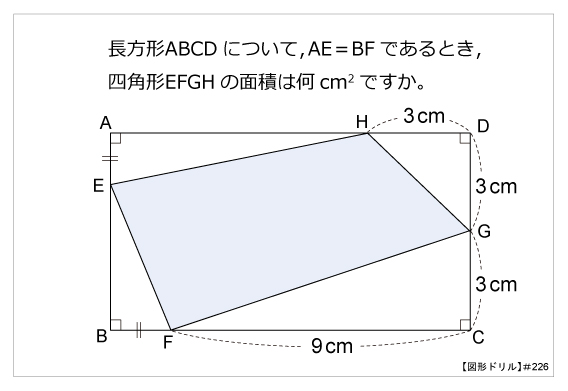
四角形gebh= geb gbh= 5 3 2= 11 3 よって四角形gebh abcd=1180 学習 コンテンツ 練習問題 各単元の要点 pcスマホ問題 数学の例題 学習アプリ 中2 連立方程式 計算問題アプリ 連立の計算問題 基礎から標準問題までの練習問題と、例題による解き方の説明四角形PLCMの面積を求めよ。 この問題に対して、右図のような補助線を引いて考えることがポイントとなる。 右図において、 四角形PLCM =四角形PKBL+四角形PMDN -四角形四角形と三角形の面積 (1) 平行四辺形と三角形の面積 平行四辺形の面積を求める公式を書きましょう。 三角形の面積を求める公式を書きましょう。 次の図形の面積を求めましょう。 ① ② ③ ④ 6㎝
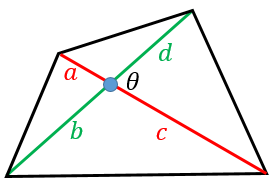



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学



四角形の面積と変換 Geogebra
このとき、四角形PABQの面積の最大値を求めよ。 (答) 3 a 2 /4 三角関数を用いて解いてみた。 等積変形により、ABとPQは平行であるとしても一般性は失われない。このとき、四角形 PABQは線分ABの垂直2等分線に関して対称な図形となる。 このとき、四角形PABQの面積をSとおくと四角形の面積を求める公式は、どれも三角形の面積を求める公式から得ることが出来ます。 四角形に 対角線 ( たいかくせん ) を引くと、三角形に分けられますよね? 面積をそのままで四角形を三角形にする作図ができました。 作図の仕方を丸暗記するんじゃなくてしっかり理解してくださいね。 等積変形を使って二等分線を書く 右のような三角形があります。 点\(P\)を通る\(\triangle ABC
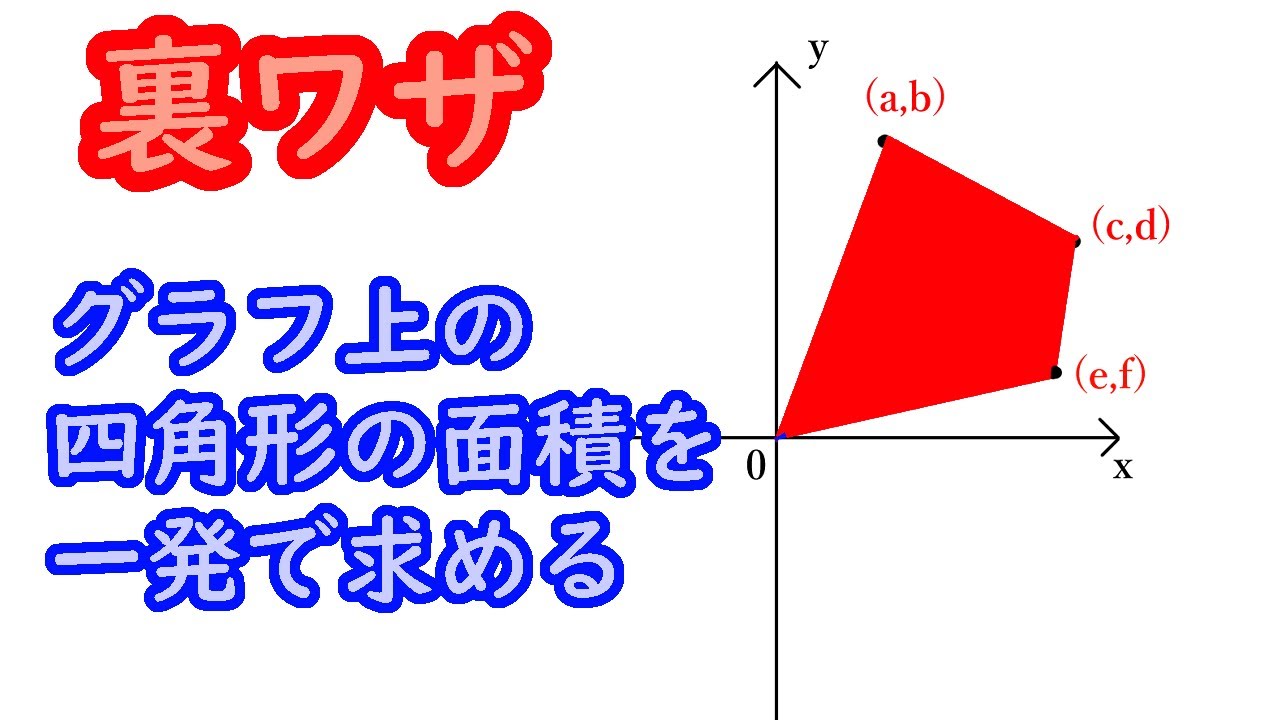



裏ワザ公式 グラフ上の四角形の面積を一発で求める方法 Youtube



四角形の面積について 小5 小6 中1 中2 中3 家庭教師とっしゅ先生の授業 小学生 中学生
右図6の凹四角形 abcd は三角形 abd から三角形 bdc を取り除いたものだから、その面積は − =12−6=6 になります。 (4) 縮尺図を用いて表しているときに実際の図形の面積を求めるには、各辺の実際の長さを求めてから計算しなければなりません。四角形の面積の計算順を守るべき理由 小学校で四角形の面積の求め方は「縦*横」と習います。 そして当然ですがこの計算結果は、順序を「横*縦」に逆転させても同じになります。 縦3cm横5cmの長方形だった場合、以下のようになります。 縦×横:3 * 5 = 15面積最大の四角形?? んなの辺の長さの合計が大きくなれば無限大に拡散するわい。 最近は無限大に収束するんだって? ワシの頃はそんな話はなかったぞ。まあ良い。 この問題が問題として成り立つには「一定の外周を持つ四角形で」最大面積になるのは



面積最大の四角形



Q Tbn And9gct8mjpenhvsxxfek Ceorhkk1e5jnkqcmelwl1yafnkyt4mflap Usqp Cau



三角形 四角形の面積比 中学から数学だいすき




平行四辺形の面積の求め方 公式と計算例



2直角四角形の面積を求める極意 すぐるゼミ




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト
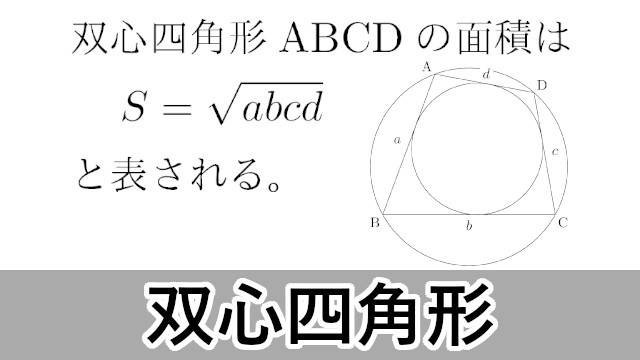



双心四角形の面積 外接円と内接円の両方をもつ四角形 大学入試数学の考え方と解法




平行四辺形の面積の求め方 公式と計算例




ポテト一郎 円に外接する四角形の面積比をまとめました T Co racutya4 Twitter
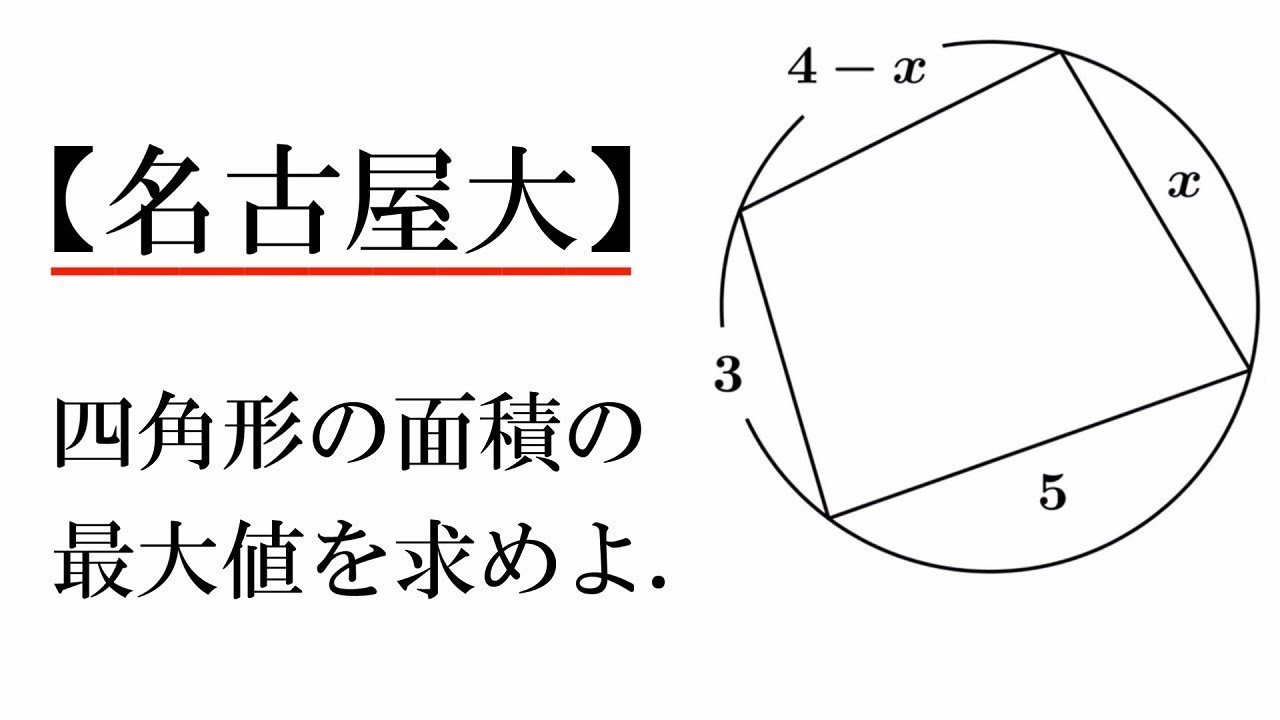



名古屋大 円に内接する四角形と三角比 超わかる 高校数学 A 演習 三角比 26 Youtube
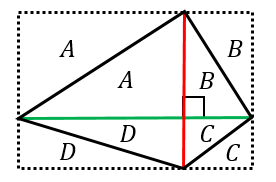



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学
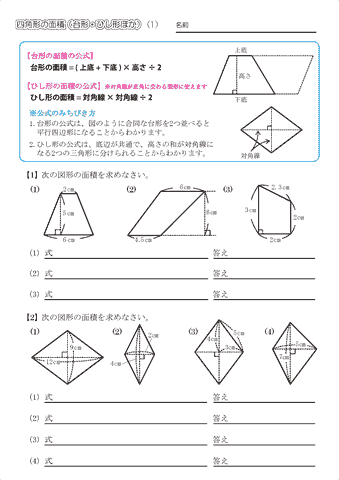



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生
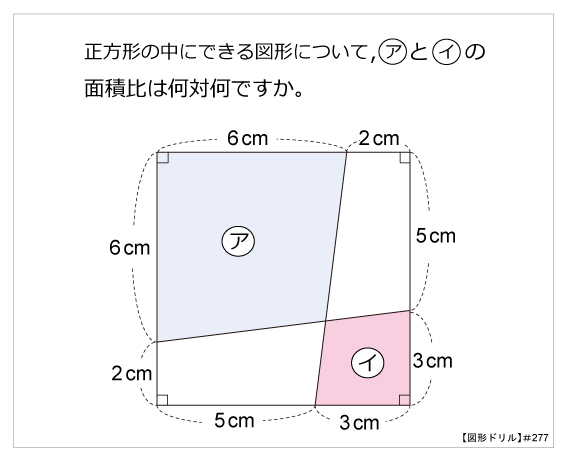



図形ドリル 第277問 2つの四角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
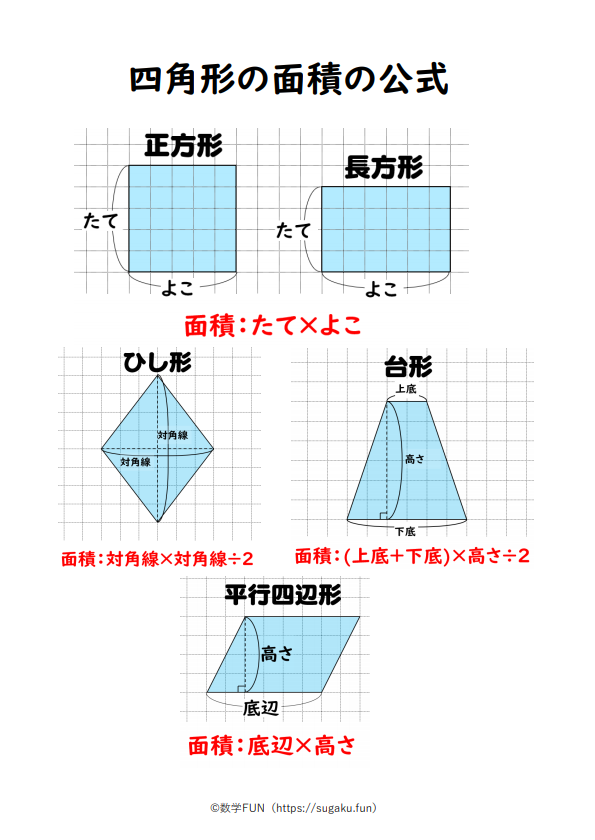



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
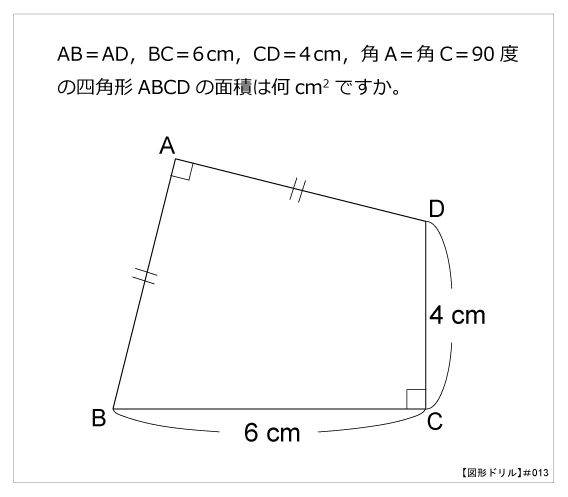



図形ドリル 第13問 四角形の面積 算数星人のweb問題集 中学受験算数の問題に挑戦



四角形の分割
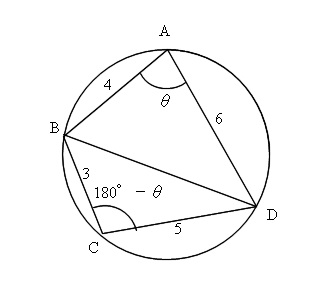



円に内接する四角形の面積の求め方と定理の使い方




平行四辺形の面積の求め方 公式と計算例



長方形の面積 算数の公式覚えてますか



Http Www News Ed Jp Gimu Yumeako Gakuryoku H24 H24syosa H24syosab 3 Pdf




4辺が与えられたとき 面積最大になる四角形は 身勝手な主張




高校数学 円に内接する四角形の対角線の長さと面積 受験の月



対角線が垂直に交わる四角形の面積の求め方 久保塾 今治市の学習塾



四角形の対角線の長さから面積を求める公式 具体例で学ぶ数学
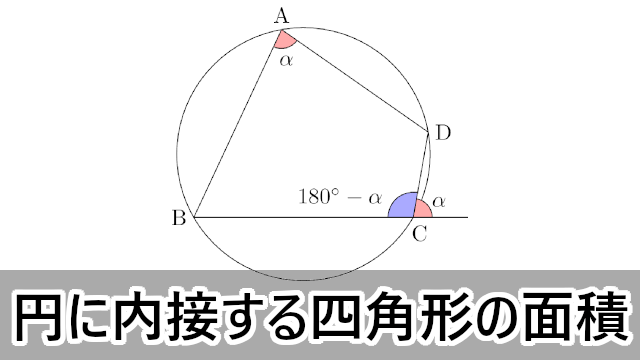



数学ia 円に内接する四角形の面積 大学入試数学の考え方と解法
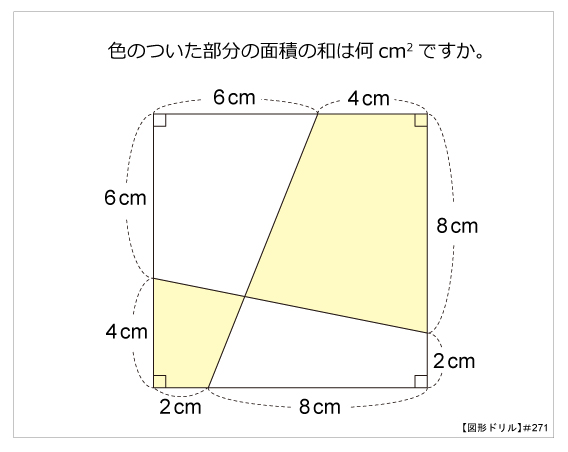



図形ドリル 第271問 四角形の面積の和 算数星人のweb問題集 中学受験算数の問題に挑戦



第13回 三角形と四角形の面積2 Youtube



4 8 長方形の中の複雑な斜線の部分の面積を求めるには さんすうがく パート 2
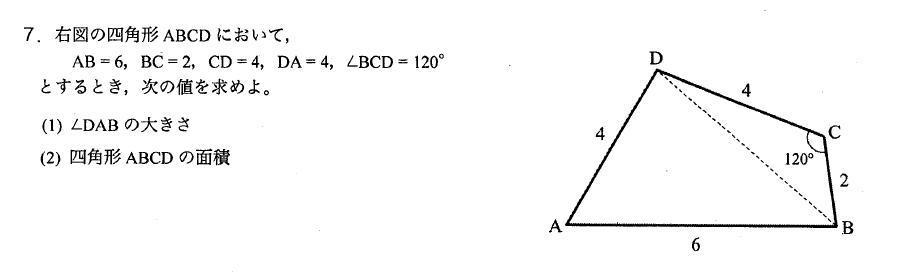



角度 四角形の面積を求める問題です 大学入試数学問題の解説 解答



小5 対角線が垂直に交わる四角形の面積 をアップ 久保塾 今治市の学習塾



3



5年 平行四辺形の面積 算数イメージ動画集 大日本図書



Mondai67




四角形の面積を二等分する直前の式ってどう求めるか教えてください Clear




吉祥女子 75度を利用して四角形の面積を求める ジーニアス 中学受験専門塾



対角線と四角形の面積 図形と計量 おおぞらラボ



図形ドリル 第226問 長方形の中の四角形 算数星人のweb問題集 中学受験算数の問題に挑戦



対角線と四角形の面積 図形と計量 おおぞらラボ



四角形の種類と面積の求め方 算数勉強会 小学 楽天ブログ



この四角形の中の三角形の面積の求め方をおしえてください A 長方形 Yahoo 知恵袋




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




四角形の対角線と面積 数学i フリー教材開発コミュニティ Ftext
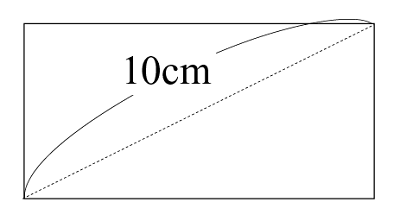



Twitterで見つけた小学校で習う知識のみで解けてしまう面積問題 恋する中学受験 大学受験を見据えた中学受験



面積の計算ドリル




面積の求め方 計算公式一覧



四角形の面積 ヘロンの公式 応用 高精度計算サイト




面積問題 小学4から6年生 算数問題プリント
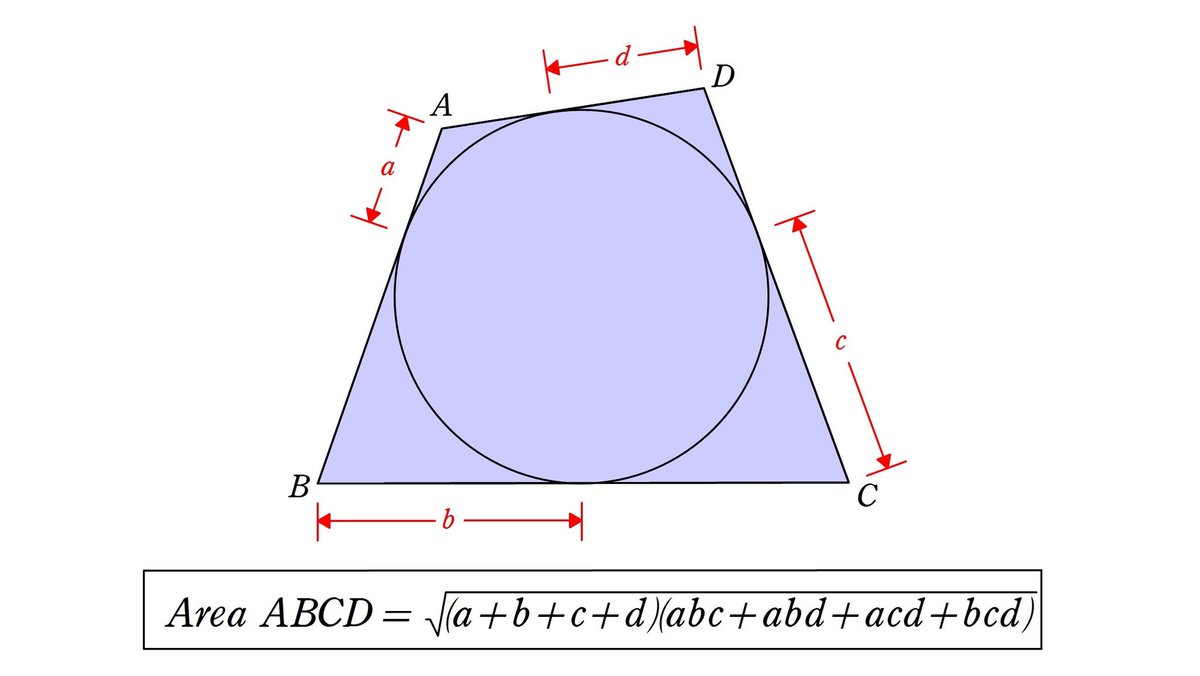



ポテト一郎 さんのツイート 円に外接する四角形の面積 なんと 角の大きさに依存しません



1



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生



松本市学研梓川教室やまと教室公式ブログ 四角形の面積の公式



小学5年生の算数 四角形の面積 台形 ひし形ほか 問題プリント ちびむすドリル 小学生




対角線から四角形の面積を求める公式を1分で証明する 怜悧玲瓏 高校数学を天空から俯瞰する
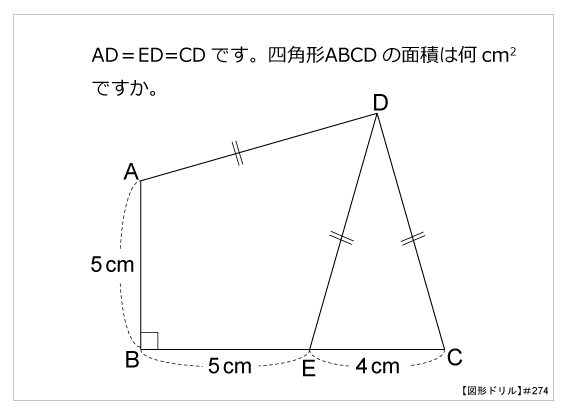



図形ドリル 第274問 四角形の面積 算数星人のweb問題集 中学受験算数の問題に挑戦




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




長方形の面積の公式 算数の公式



教育ソフト開発研究所 5年5巻




高1 四角形の面積 ブラーマグプタの公式etc 高校生 数学のノート Clear
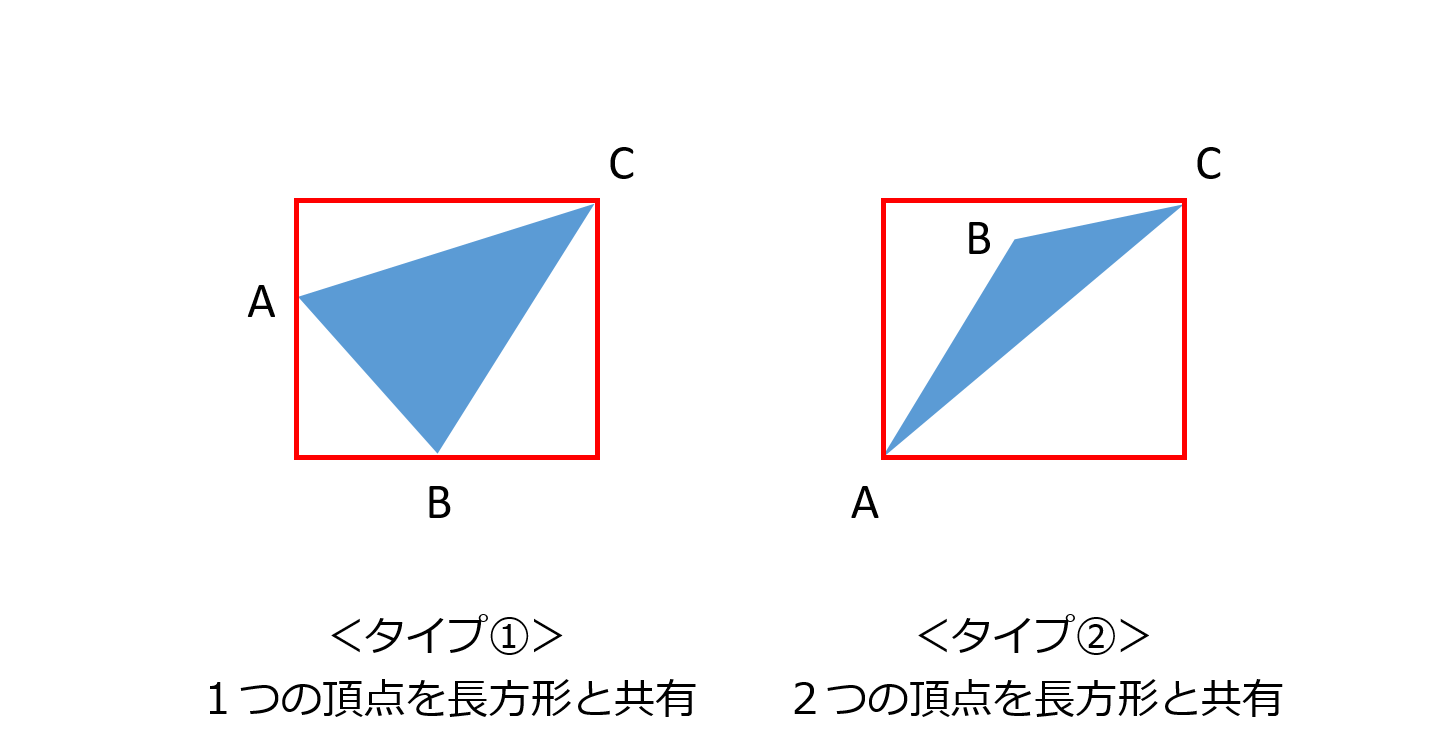



正方形の中にある三角形の面積の平均の求め方 三角形を分解して組み立てなおす Musyokutoumei



四角形と面積比 べっこう色の記録



四角形の面積 式から形を求めよう




すきるまドリル 小学5年生 算数 図形の面積 無料学習プリント すきるまドリル 無料学習プリント



円に内接する四角形の面積を求める公式 具体例で学ぶ数学



3




長方形の面積の求め方 簡単な計算問題で公式を覚えよう 中学や高校の数学の計算問題



四角形abcdの面積は 灘中学 過年度 パズル算数クイズ



この四角形の面積の求め方を教えてください 難しいことを考えず普通に考 Yahoo 知恵袋




簡単公式 長方形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



四角形の面積を求めたいとき 4辺の長さが分かっているだけでは面積を Yahoo 知恵袋
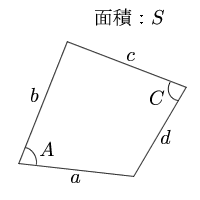



四角形 4辺と対角の和 面積の計算 計算サイト
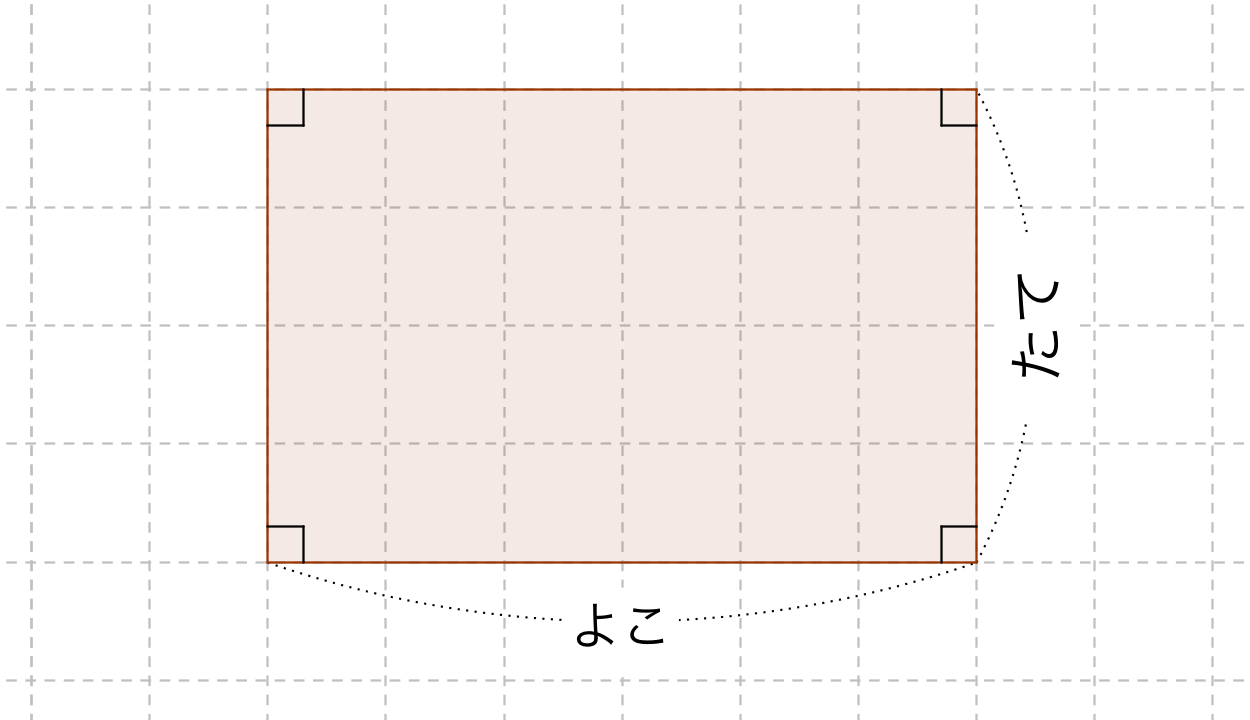



長方形の面積の公式 算数の公式




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




問題96 四角形の面積




基本のquadrilaterals 四角形 の英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強
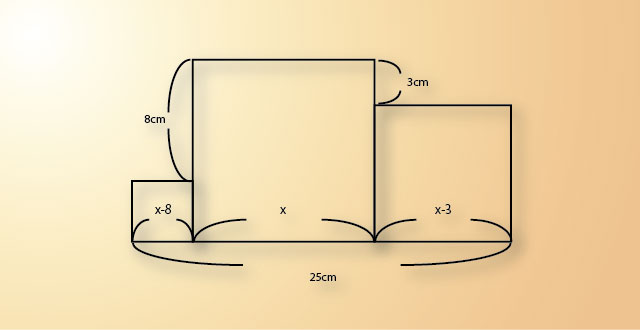



大きさの違う3つの正方形を並べた形の面積を求める問題の2種類の解答方法 非天マザー By B Chan




高校数学テクニック集 002 数学 A 三角比 四角形の面積を求める公式 大学受験対策 数学i 図形と計量 学習塾 Dear Hope ディアホープ 改訂 Youtube
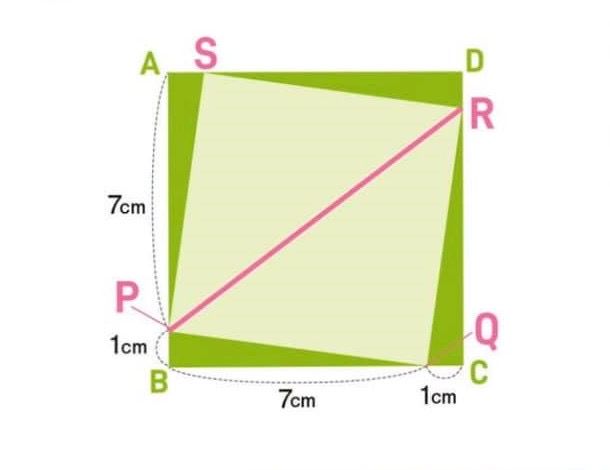



小学校で習う 四角形の概念 と 面積の公式 だけ で解いてみよう 解答編 Npo Selfish セルフィッシュ
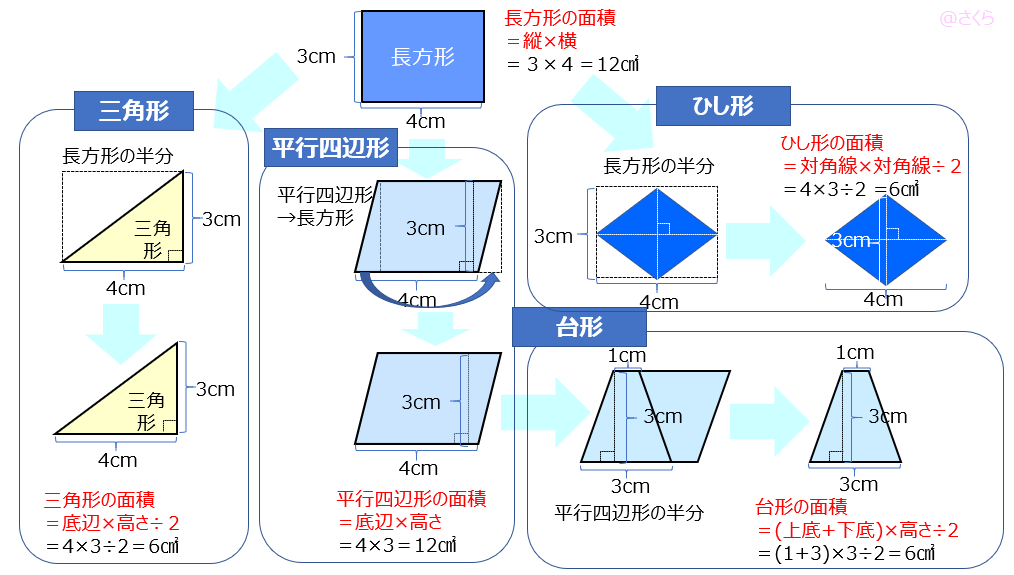



四角形の種類と性質 面積の公式について 中学受験 ゲーム大好き息子の偏差値32からの挑戦



四角形の面積




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun



Kids Gakken Co Jp Box Sansu 05 Pdf B Pdf



正方形と長方形の面積 家庭学習レシピ



四角形の面積を4辺から求める 面積計算機




円に内接する四角形の面積をサインを使って求める問題 数学i By ふぇるまー マナペディア
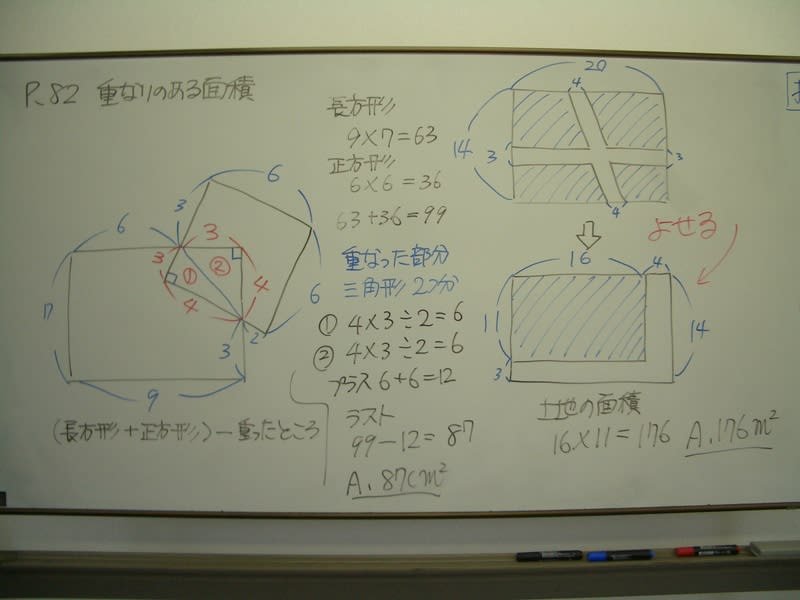



小5算数 重なりのある面積 ブログ アビット




算数 131 特別な四角形の面積を求める 高輪 平面図形 Youtube
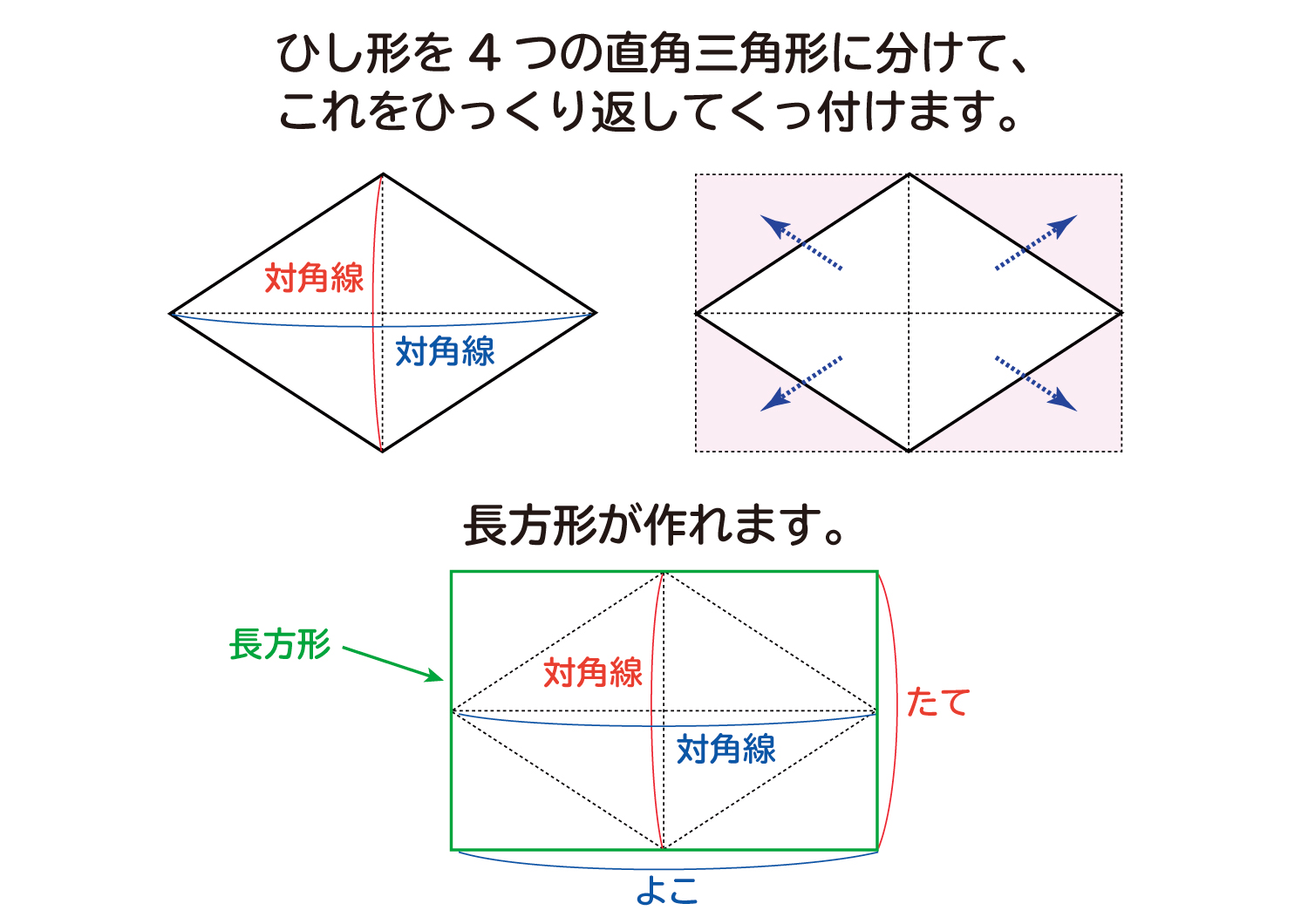



なぜ ひし形の面積は 対角線 対角線 2 なのか を説明します おかわりドリル




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
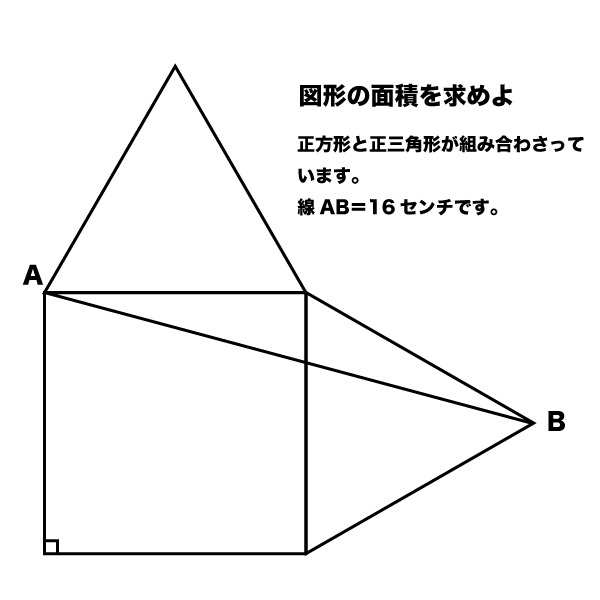



正方形と正三角形が組み合わさった図形の面積計算 受験算数入門



算数 四角形の面積 応用問題 解答 なるほどの素




Twitterで見つけた数学の問題 四角形の面積 Soutai 40



0 件のコメント:
コメントを投稿